本文记录一些基本数学运算的算法。
内容包括:
本文内容较多,需要读者静心阅读。
整数加法 ¶
不用加减乘除四则运算符,如何编程实现加法?
回顾熟悉的十进制加法的竖式计算:
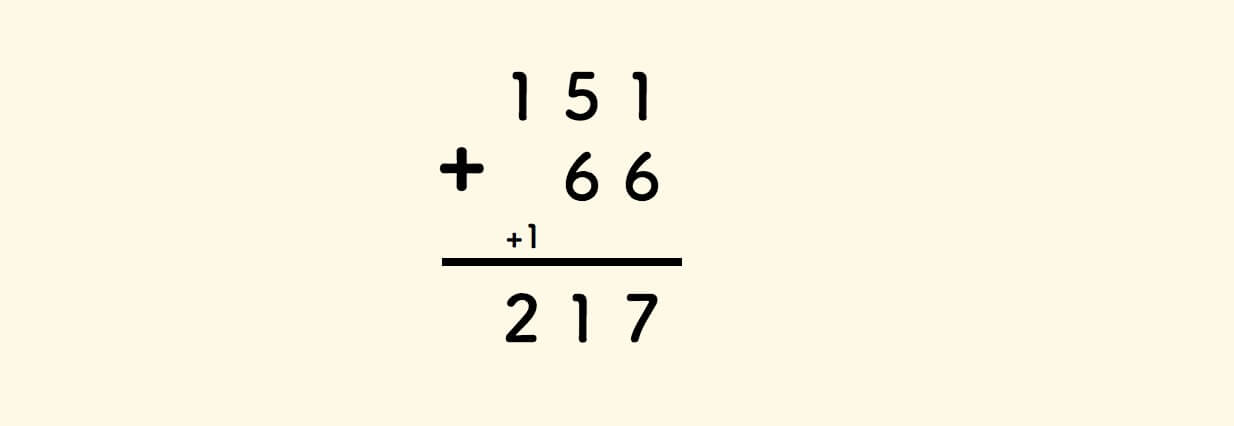
二进制加法也是类似的,满二进一:
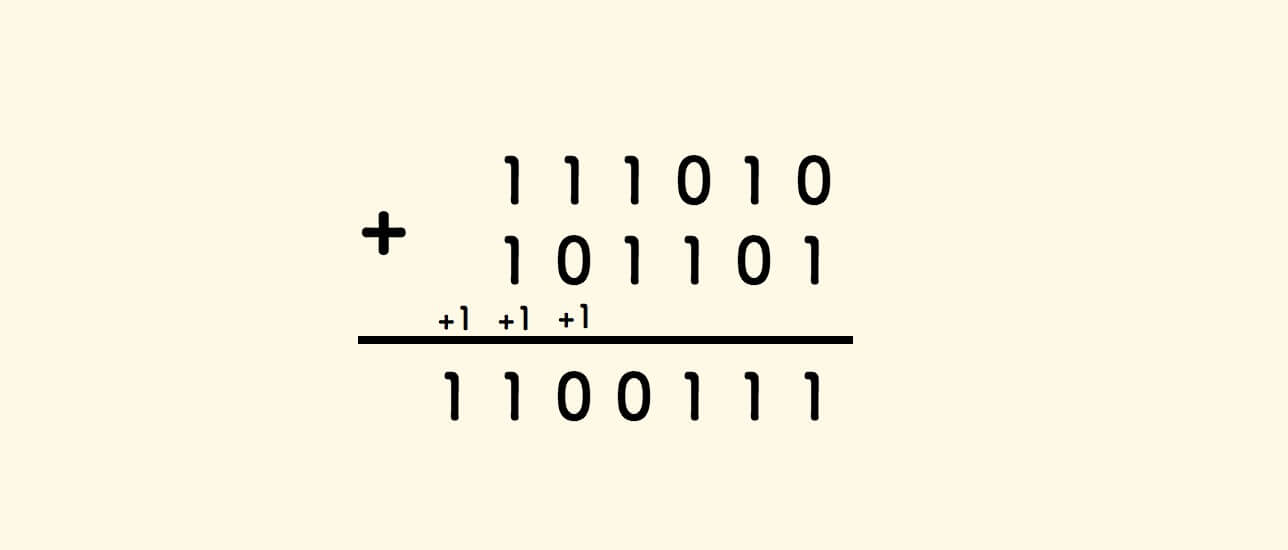
把进位的一栏记为 c ,不考虑进位的和记为 s 。
如果上一位的比特值之和满二,则下一位 c 记 1 ,s 则只记录当前位的和的比特值。
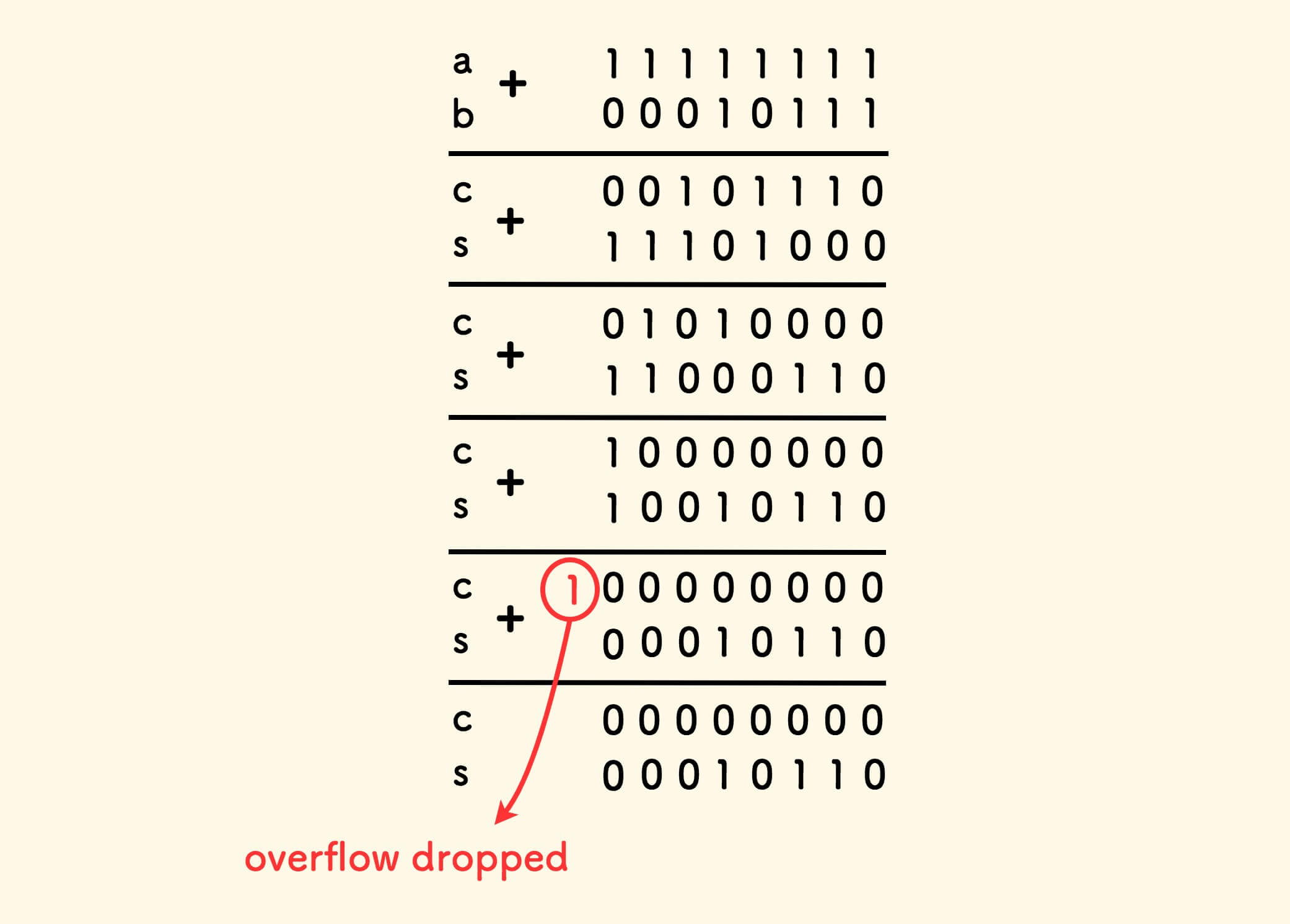
如此一来,上面的二进制竖式计算拆解如下:

可以看到,不断迭代竖式计算,直到进位 c 为 0 的时候,s 即最终的计算结果。
在每一栏位上,下一位的 c 和当前位的 s 的计算表格如下:
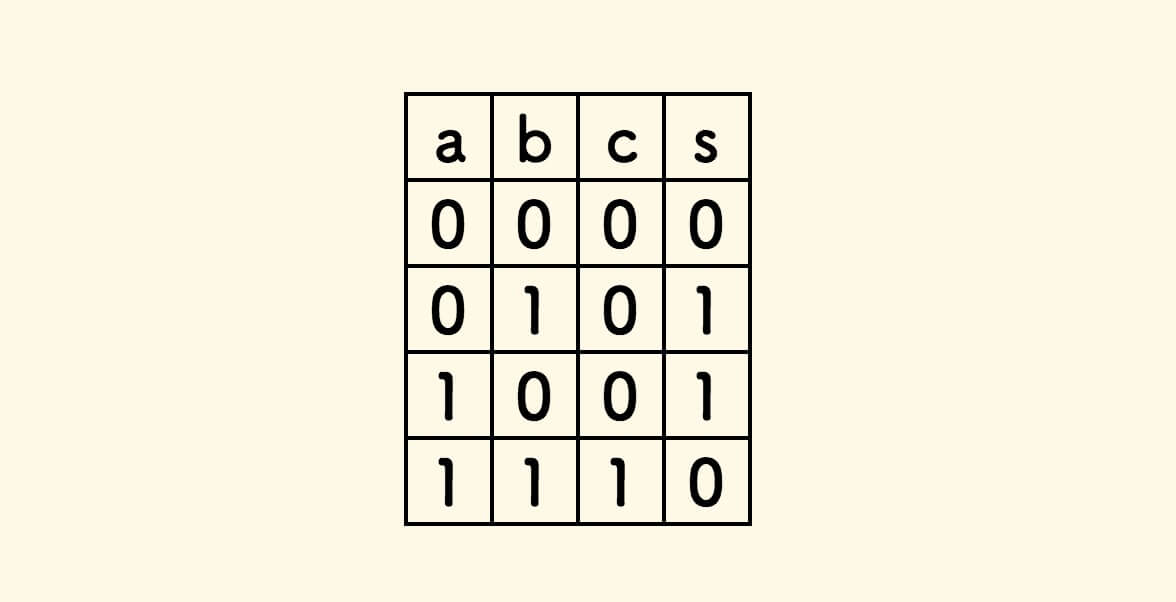
仔细观察,可知 c 的值其实是「逻辑与」的结果,s 的值其实是 「逻辑异或」的结果:
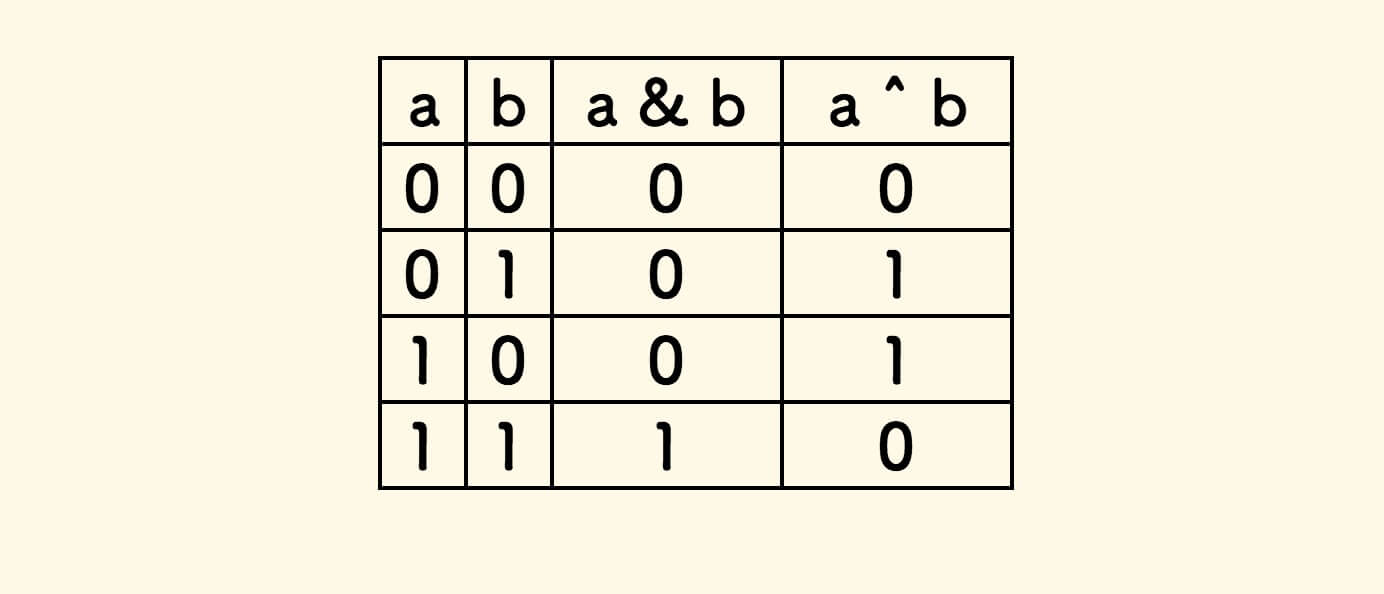
因此,c 的数值可以表达为 (a & b) << 1 ,s 的数值可以表达为 a ^ b 。
每次计算出 c 和 s 后,把 c 当做新的 a ,s 当做新的 b , 不断循环迭代,直到 a 为 0 ,就得出最终计算结果 b 。
这个方法对负整数是否成立呢?负数的最高位是符号位 1 ,下面是 8bit 负整数 -1 和 23 = 10111 的结果:
算法仍然适用,事实上,在二进制上,负数无非即大正数。
加法的位运算实现 - C 语言
// 加法
int Add(int a, int b) {
do {
int c = (unsigned int)(a & b) << 1;
int s = a ^ b;
a = c;
b = s;
} while (a != 0);
return b;
}
以上算法中,每次左移一位,时间复杂度是 O(k) ,k 是两个整数的较大的比特位数。
时间最坏情况下,当进位最多的时候。下图是 4bit 整数情况下的算法最差情况的示例图, 计算 -1 和 1 相加的过程,需要 4 步完成。

对于 32bit 有符号整数来讲,最坏情况则需要 32 步完成。
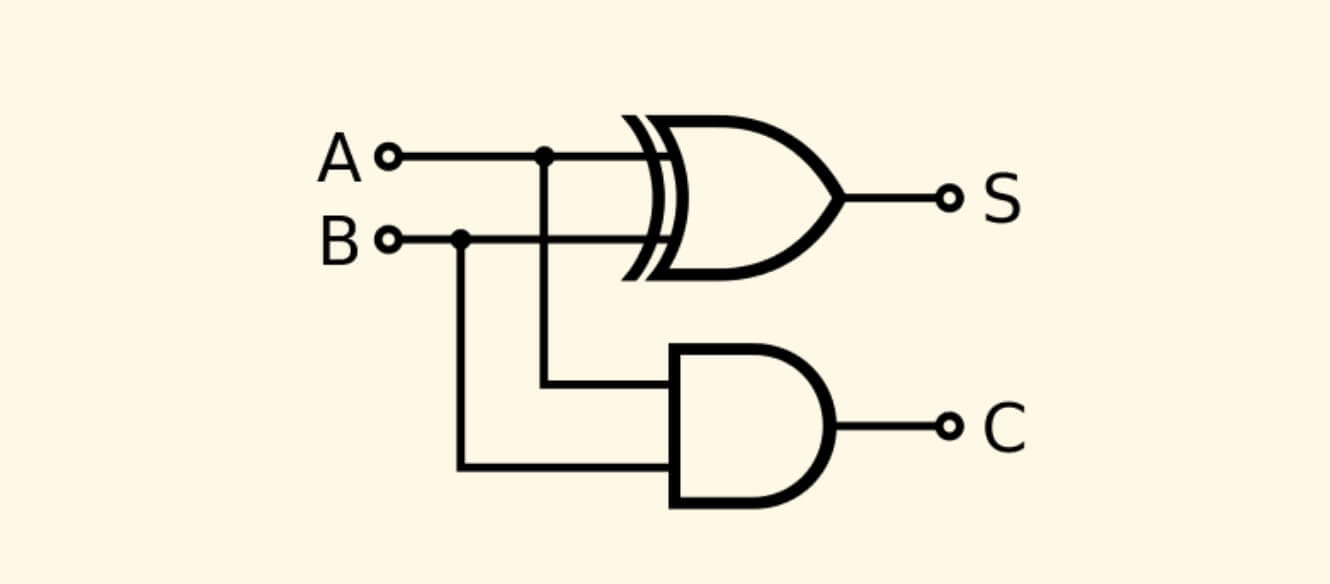
事实上,这个方法和计算机中 加法器 的实现非常类似。
一位半加器 接收两个比特的输入,经过 异或门 输出当位的和 S ,经过 与门 输出进位 C 。
整数减法 ¶
减法,可以用加法来表达, a - b = a + (-b) 。
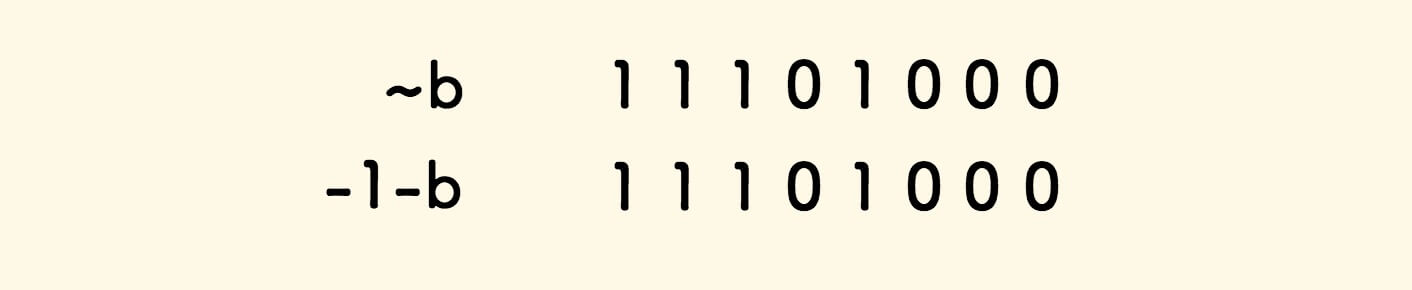
以 8bit 有符号整数为例,假如 b = 10111 ,那么 -b 可以如下得出:

又因为 -1-b 其实就是 ~b ,所以 -b = ~b+1 。
因此 a - b = a + (~b+1) ,即 Minus(a, b) = Add(a, Add(~b, 1)) 。
减法的位运算实现 - C 语言
// 减法
int Minus(int a, int b) { return Add(a, Add(~b, 1)); }
整数乘法 ¶
乘法即是循环的加法,不过如此计算的话,时间复杂度是 O(min(a,b)) 。
乘法的循环加实现 O(min(a,b)) - C 语言
#define MIN(a, b) (a) > (b) ? (b) : (a)
#define MAX(a, b) (a) > (b) ? (a) : (b)
// 乘法 - 简单方法 O(min(a,b))
// 假设加法已经实现
// 以下只考虑正数实现,负数可转正数处理
int MulNaive(int a, int b) {
int min = MIN(a, b);
int max = MAX(a, b);
int r = 0;
while (min-- != 0) r += max;
return r;
}
快一些的办法是,二分法。
举例来说,13x17 的计算过程可以拆解如下:
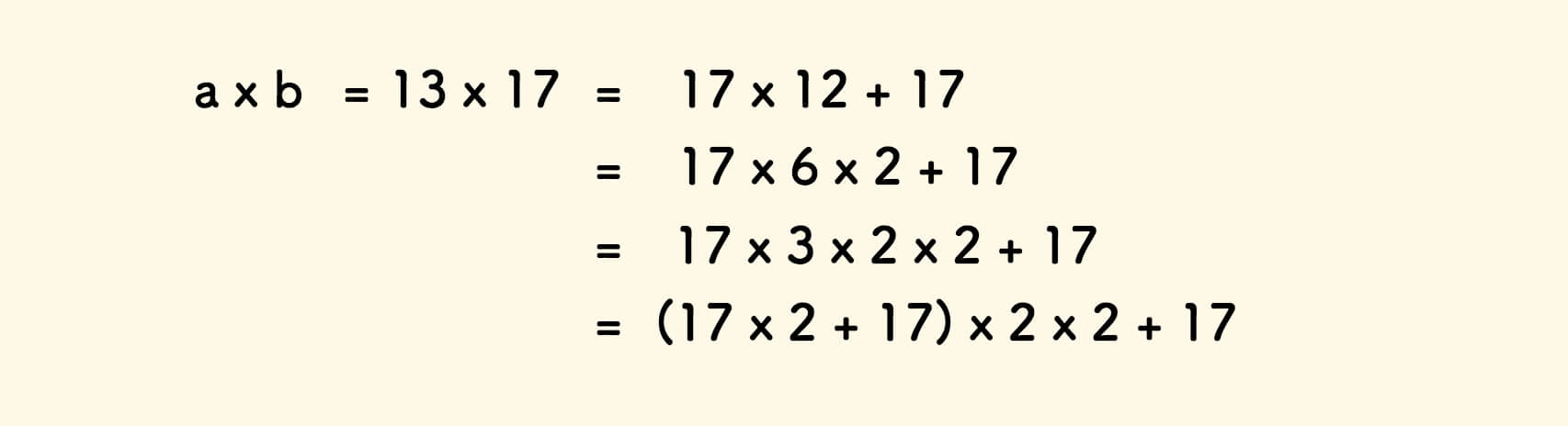
拆解过程中,把 a 当成了倍数,b 当成了被乘数。
如果倍数是偶数,则二分倍数,否则化倍数为偶数。
容易得出此方法的递归版本:
乘法的二分法实现 - 递归版本 - C 语言
// 乘法 - 二分法 递归版本
// 以下只考虑正数实现,负数可转正数处理
int MulRecursive(int a, int b) {
int min = MIN(a, b);
int max = MAX(a, b);
if (min & 1) // 奇数
return MulRecursive(min - 1, max) + max;
else { // 偶数, 注意 min/2 即 min >> 1
int half = MulRecursive(min >> 1, max);
return half << 1; // 即 half x 2
}
}
另外一种视角,是把 a x b 分解为三个部分:
- 计算结果
result - 乘式因式
factor - 剩余倍数
remain
构成方式是 a x b = result + factor * remain 的形式。

尝试不断减少剩余倍数:
- 如果是偶数,则分解一个
2到左边的乘式因式factor中, 即factor增大一倍,剩余倍数减半。 - 如果是奇数,则分解一个被乘数
factor加到左边的result中,剩余倍数减一。
当剩余倍数缩减到 0 时,result 则积累到最终结果。
下面是这种算法的一种最好情况,剩余倍数不断减半:
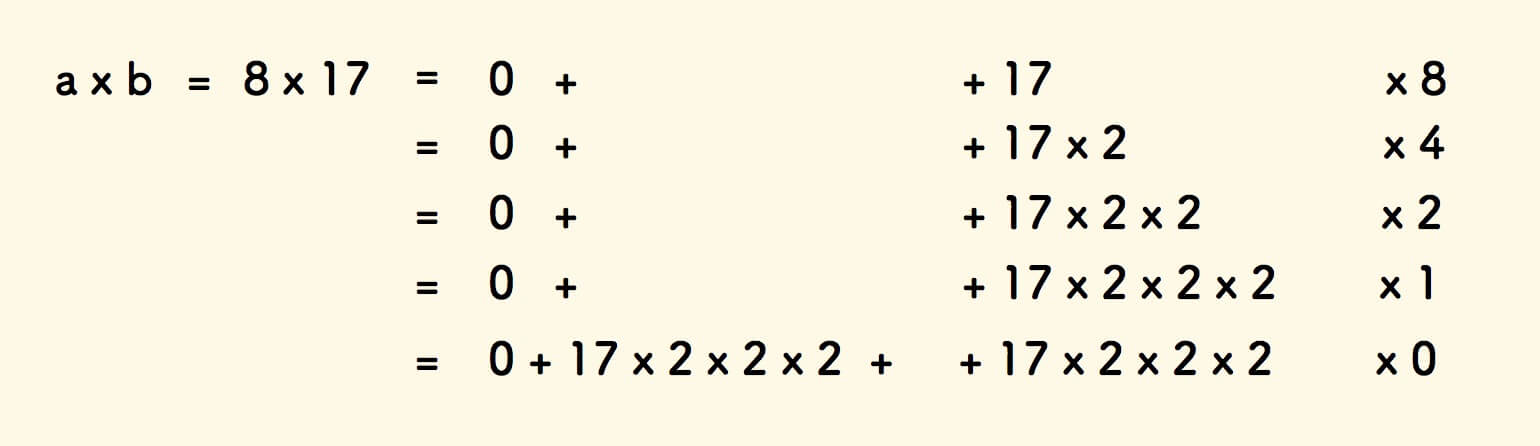
乘法的二分法实现 - 循环版本 - C 语言
// 乘法 - 二分法循环版本
// 以下只考虑正数实现,负数可转正数处理
int MulBinary(int a, int b) {
int min = MIN(a, b); // 小的作倍数
int max = MAX(a, b); // 大的作被乘数
int r = 0; // 计算结果
int factor = max; // 乘积因子
int remain = min; // 剩余倍数
while (remain != 0) {
if (remain & 1) {
// 剩余倍数为奇数
r += factor;
remain--;
} else {
remain >>= 1; // 剩余倍数缩小一半
factor <<= 1; // 被乘数扩大两倍
}
}
return r;
}
显然,时间复杂度是 O(logn) ,其中 n 是 a 和 b 中较小的一个数。
最后一种思路,回想一下十进制数的乘法竖式:
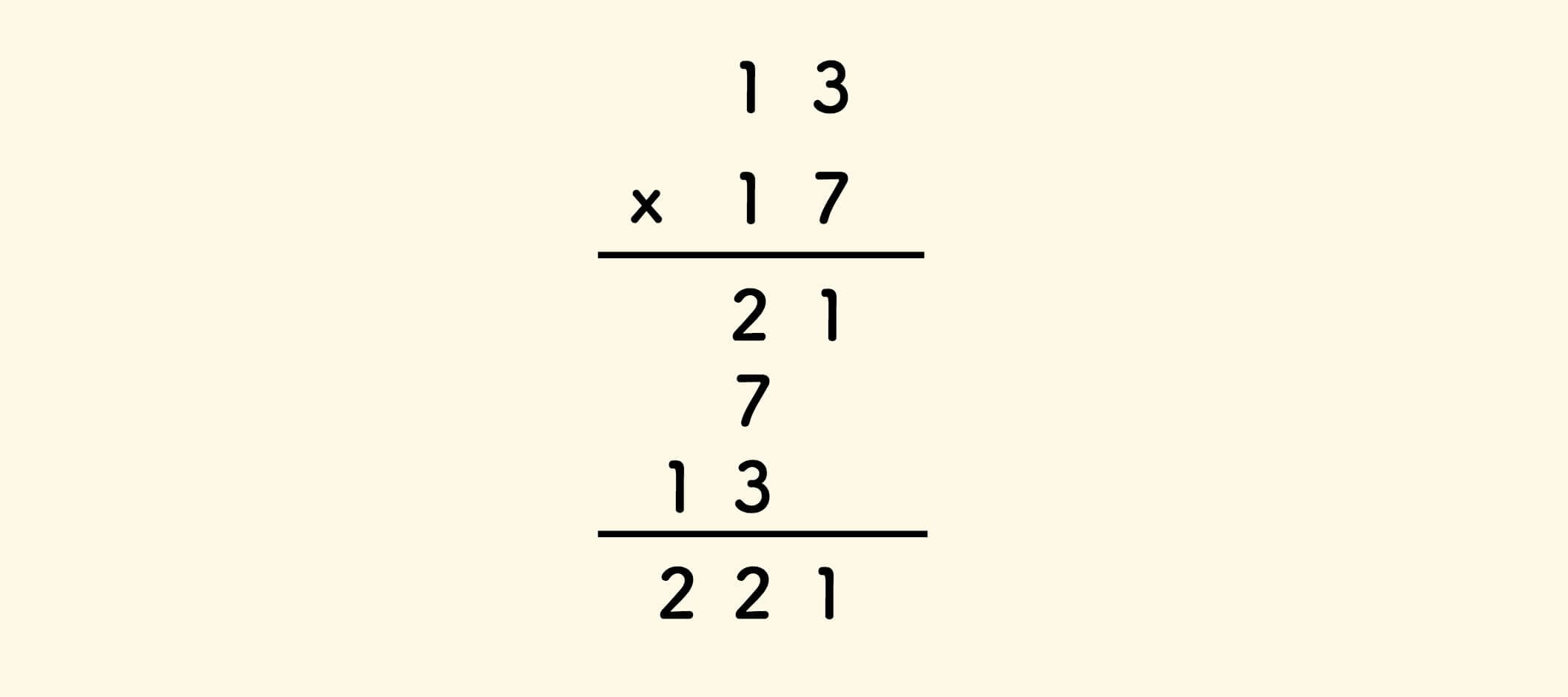
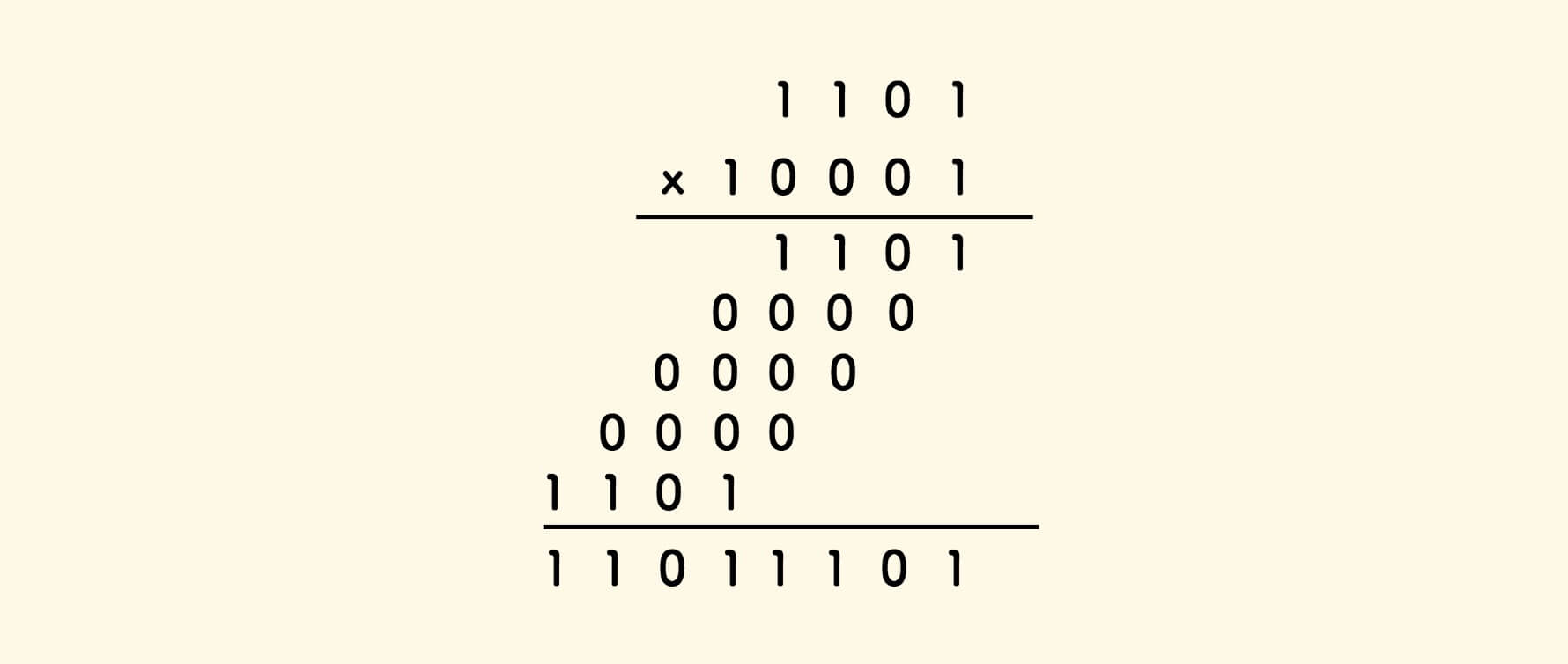
二进制的乘法竖式,是这样的:
相比十进制乘法,它更简单,0 乘以任何数是 0 ,1 乘以任何数是自身, 用不到乘法九九算术表:
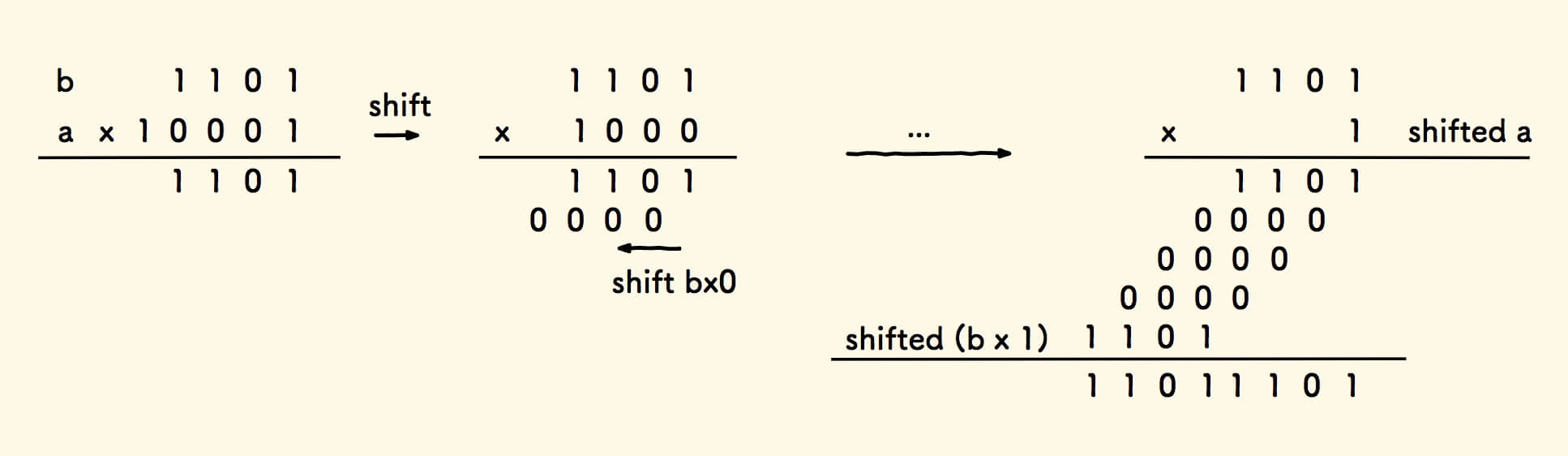
假设 a 和 b 的比特位数是 k 和 m , 把一个数字 b 不断左移 k 次,得到的数求和即乘法结果。
具体来说:
- 不断右移数字
a,直到它为0时,即移动了k次。 - 每次右移数字
a后,其当前最后一位是a & 1,和数字b相乘:0乘以任何数是0, 因此不需要处理这种情况。1乘以任何数是自身 ,只需要处理这种情况。- 将乘积左移一位,加到计算结果求和。
即得所谓的快速乘算法。
乘法的二进制竖式思路的实现 - C 语言
// 乘法 - 竖式计算方法
// 以下只考虑正数实现,负数可转正数处理
int MulFast(int a, int b) {
int r = 0; // 乘法结果
while (a != 0) {
if (a & 1) {
// 当前位是 1, 1 乘以任何数为自身
// 加上此时的 b
r += b;
}
// 否则,当前位是 0, 0 乘以任何数是 0, 无需加上
a >>= 1; // 移动 k 次到 0 意味着 a 有 k 个比特位
b <<= 1; // 同步左移 b
}
return r;
}
容易知道,此算法的时间复杂度是 O(k), k 是整数 a 的比特位数。
注意,此处所说的所有的乘法时间复杂度,是在不考虑加法时间开销的意义上而言的。
整数除法 ¶
和 乘法 的分析思路类似, 容易的办法是,化除法为循环的减法。
此处 O(n) 时间复杂度的算法从略。
考虑 255 / 17 的结果,和 乘法 类似,把计算式拆解为如下形式:
其中:
- 被减的因式系数
factor: 每次增大两倍,如果remain不足,则factor重置1。 - 剩余的被除数
remain: 被除数不断被减后的剩余部分。 - 计算结果
result:每次增长factor大小。

当被除数剩余部分 remain 不足 b 大小时,终止算法过程。
除法的二分法实现 - C 语言
// 以下只考虑正数实现,负数可转正数处理
int Div(int a, int b) {
int remain = a;
int factor = 1;
int bfactor = b; // b x factor.
int result = 0;
while (remain >= b) {
if (remain < bfactor) {
// 被除数不足以相减,重置 factor
factor = 1;
bfactor = b;
}
remain -= bfactor;
result += factor;
// factor x2
factor = factor << 1;
// bfactor x2
bfactor = bfactor << 1;
}
return result;
}
时间复杂度是 O(logn) 。
另外一种思路,是源于除法竖式。
回顾十进制的除法竖式计算方法:
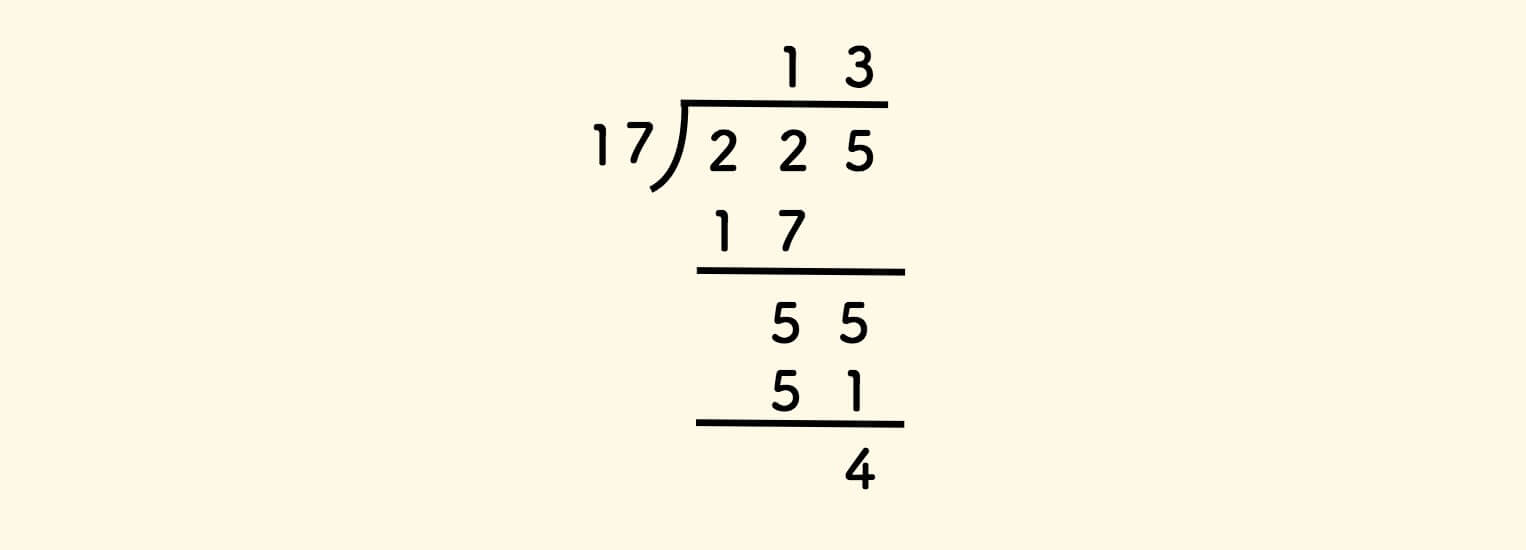
二进制的竖式除法也是一样的:
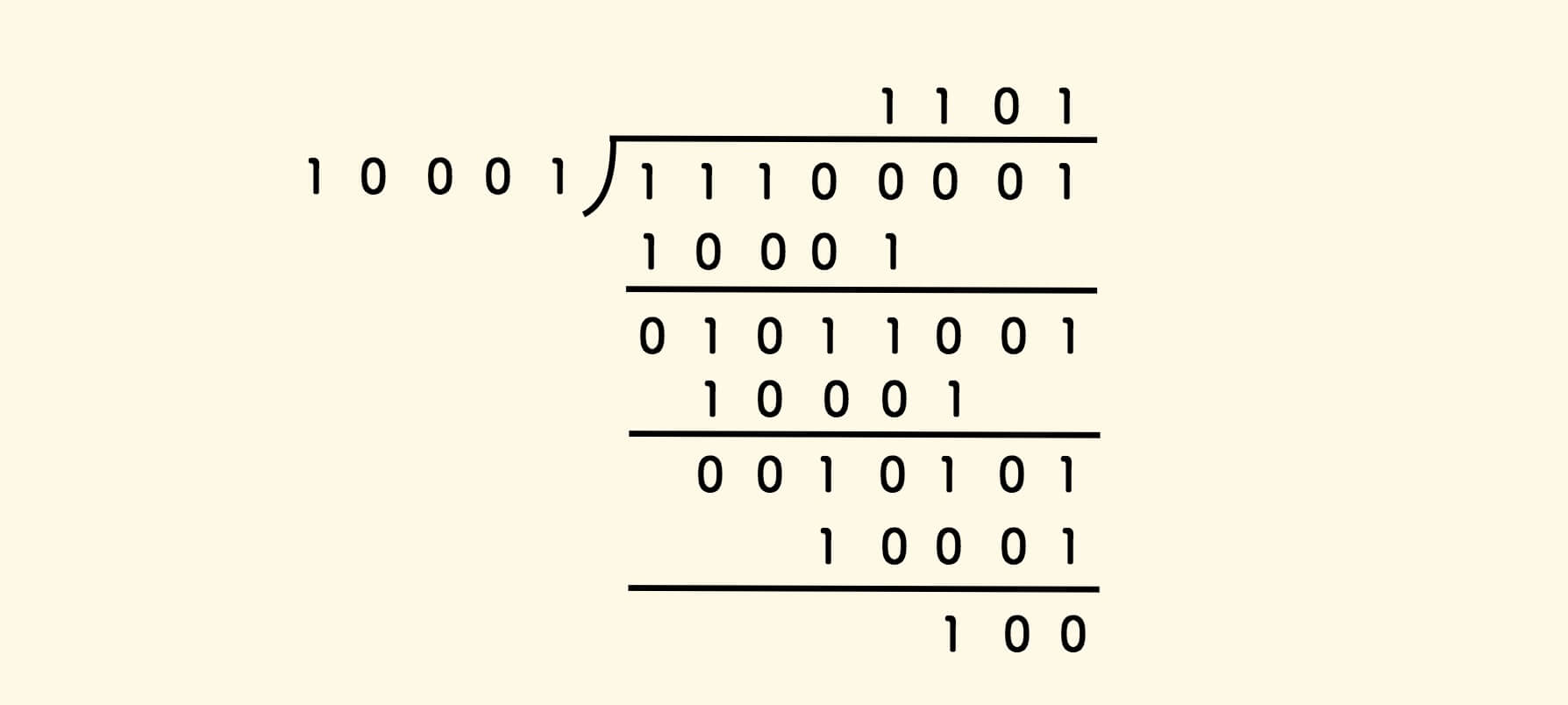
算法的思路则是:
- 初始化,
r为除法结果。 - 左对齐
a和b的有效比特起始位。 - 如果对齐后,
b不大于a,则更新被除数a = a-b,同时r的当前位标1。 - 否则,
r的当前位标0。 - 到两个数右对齐为止,结束计算。
此算法的时间复杂度是 O(k) ,k 是两个整数的较大的比特位数。
除法的竖式思路实现 - C 语言
// 获取给定整数的比特位数
int GetNBits(int a) {
int n = 0;
while (a) {
a >>= 1;
n++;
}
return n;
}
// 除法 竖式计算
// 以下只考虑正数实现,负数可转正数处理
int DivFast(int a, int b) {
int n = GetNBits(a);
int m = GetNBits(b);
int r = 0; // 计算结果
for (int i = n - m; i >= 0; i--) {
// 左移 b 对齐当前的 a
int b1 = b << i;
if (b1 <= a) {
// 标记结果的第 i 位为 1
r |= (1 << i);
a -= b1;
}
// 否则,r 的当前位标 0,即不用设置
}
return r;
}
注意,此处所说的所有的除法时间复杂度,是在不考虑加减法时间开销的意义上而言的。
快速幂 ¶
快速幂的算法和前面所说的 乘法 的分析思路是类似的。
以 3^13 为例,展开如下:
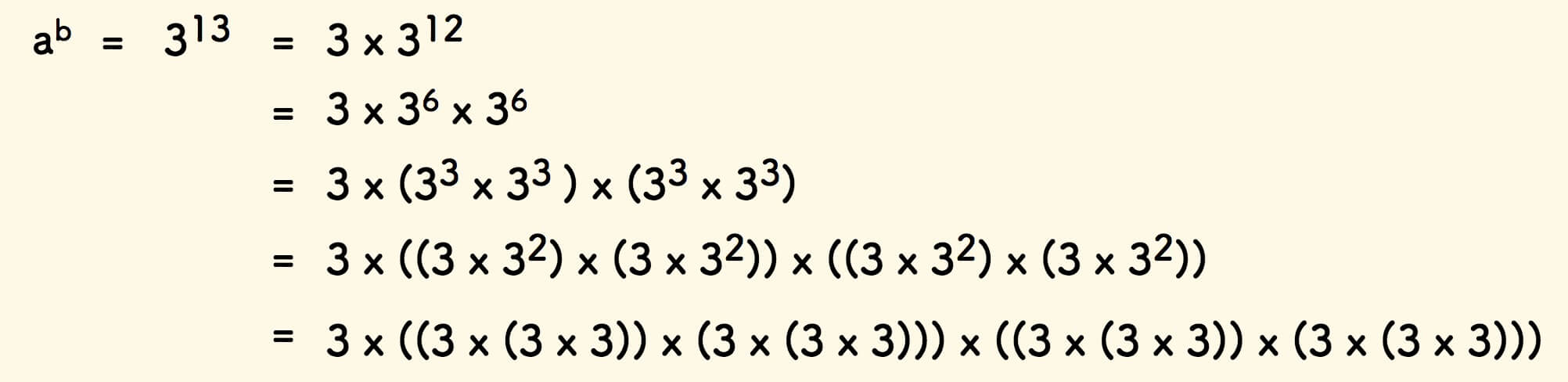
容易得出二分法的递归版本:
幂运算的二分法递归版本 - C 语言
// 幂运算 - 二分 递归版本
// 以下只考虑正数实现,负数可转正数处理
int PowRecursive(int a, int b) {
if (b == 0) return 1;
// 奇数
if (b & 1) return PowRecursive(a, b - 1) * a;
// 偶数
else {
int half = PowRecursive(a, b / 2);
return half * half;
}
}
时间复杂度是 O(logb) ,其中 b 是幂次。
不过下面的循环迭代思路的方法更为美妙。
和 乘法 的拆解思路如出一辙, 把 a^b 写成 result * (factor) ^ remain 的形式:

- 如果剩余指数
remain是奇数,则分解一个因子factor给到左边的result。 - 否则,把
remain拆半,factor自乘翻倍。
当剩余指数 remain 到达 0 的时候,result 就拿到了结果。
幂运算的二分法循环版本 - C 语言
// 幂运算 - 二分 循环版本
// 以下只考虑正数实现,负数可转正数处理
int PowFast(int a, int b) {
int factor = a;
int result = 1;
int remain = b;
while (remain > 0) {
if (remain & 1) {
// 奇数
result = result * factor;
remain--;
} else {
// 偶数
remain = remain / 2; // 剩余指数拆半
factor = factor * factor; // 因子自乘翻倍
}
}
return result;
}
时间复杂度仍然是 O(logb) ,其中 b 是幂次。
注意,此处所说的所有的幂运算时间复杂度,是在不考虑乘除法时间开销的意义上而言的。
快速幂经常会带一个模运算,下面是 PowFastMod 的实现:
幂运算的二分法循环版本 - C 语言
// 带模运算的快速幂
// 注意,模运算对乘法满足分配律 (x*y)%m=(x%m * y%m)%m
int PowFastMod(int a, int b, int mod) {
int factor = a % mod;
int result = 1;
int remain = b;
while (remain > 0) {
if (remain & 1) {
// 奇数
result = result * factor % mod;
remain--;
} else {
// 偶数
remain = remain / 2; // 剩余指数拆半
factor = factor * factor % mod;
; // 因子自乘翻倍
}
}
return result % mod;
}
平方根 ¶
如何求解 $\sqrt a$ 的值? 已知 $a >= 0$ 。
由于函数 $x^2$ 在 $x >= 0$ 区间上是单调递增的,因此可以采用二分法, 和 标准的二分查找 差不太多,介绍从略。
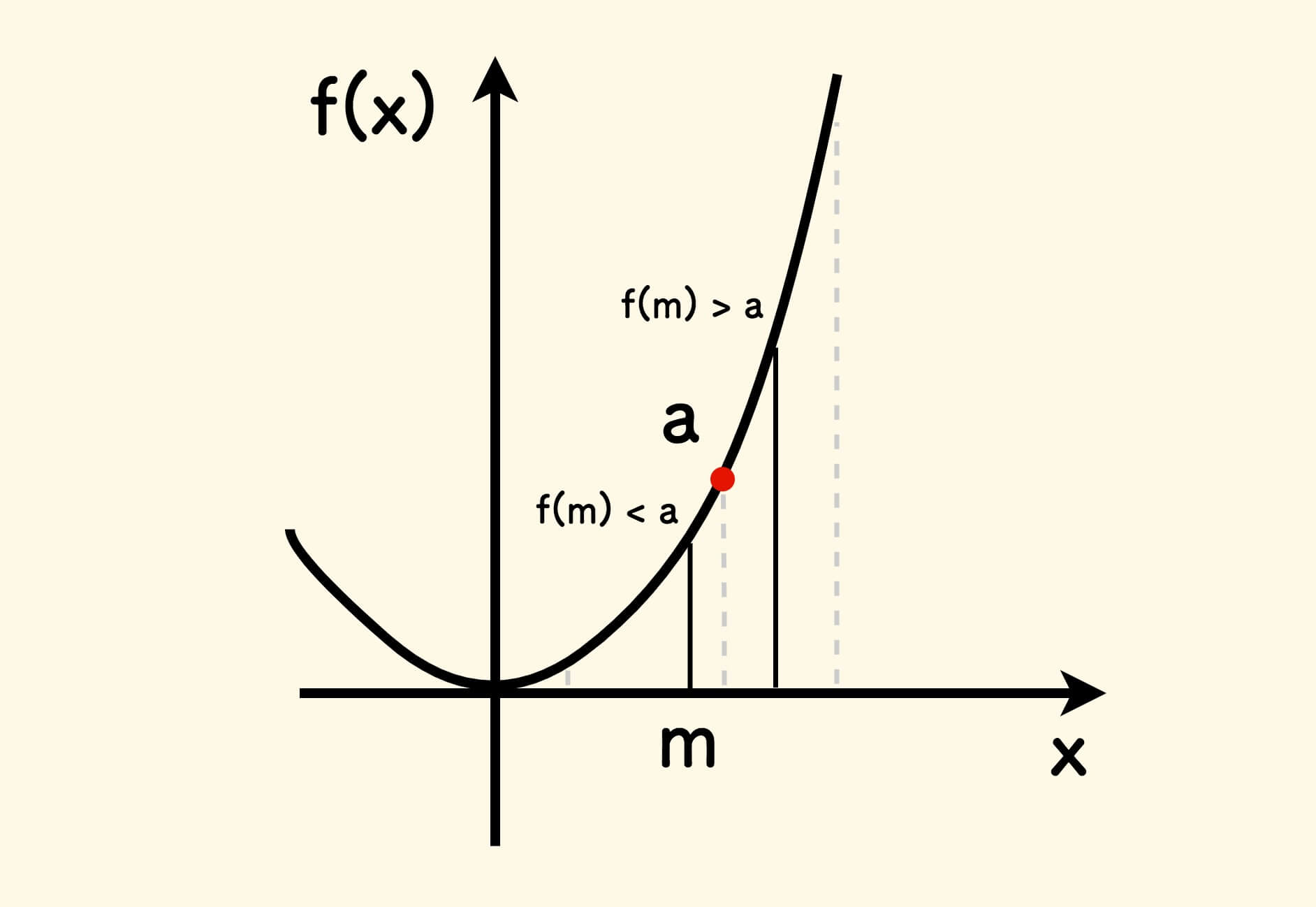
平方根运算 - 二分法 - C 语言
// 平方根运算 - 二分
// a 为非负数
int Sqrt(int a) {
if (a == 0) return 0;
if (a == 1) return 1;
int l = 0;
int r = a;
while (l < r) {
int m = (l + r) / 2;
if (m < a / m) { // 不采用 m * m < a 防止溢出
l = m + 1;
} else if (m > a / m) {
r = m - 1;
} else {
return m;
}
}
// 找到的 l 有可能比实际值稍大
if (l > a / l) return l - 1;
return l;
}
在 数值分析 中, 求函数近似零值的有一个常用的方法:牛顿迭代法 。
求解 $\sqrt a$ 的值,其实即求函数 $f(x) = x^2 - a$ 的零值。
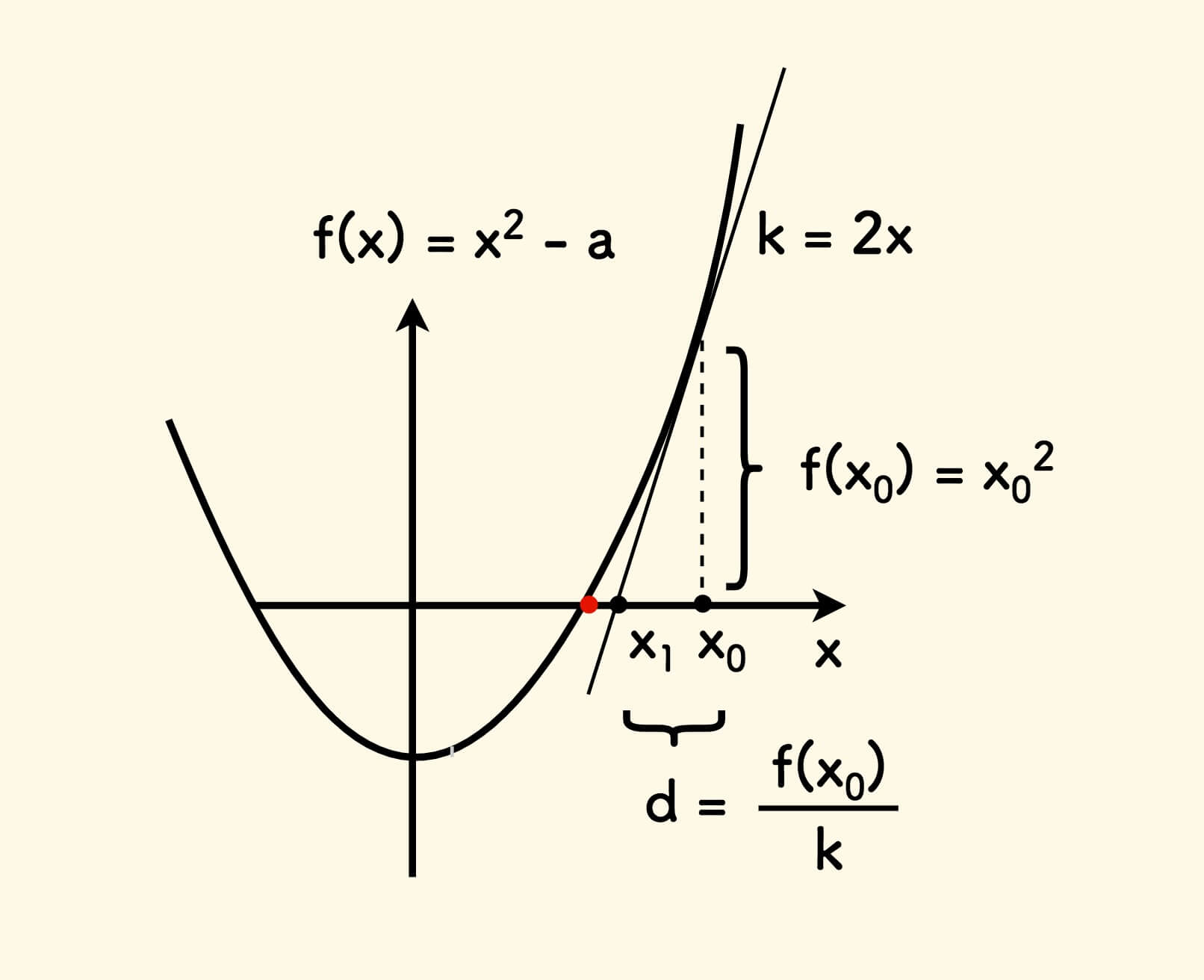
牛顿法的思路是,先取一个值 $x = x_0$ ,然后在这一点做函数的切线,将切线和横轴的交点 $x_1$ 作为 $x$ 的新值,不断迭代,直到 $f(x)$ 和零的误差满足精度要求。
切线的斜率 $k$ 可以由函数的导数 $f’(x) = 2x$ 计算得出,即 $k = 2x_0$ 。 因此:
\[x_1 = x_0 - \frac {f(x_0)} {f'(x_0)}\]按照这个方式迭代下去即可。
平方根运算 - 牛顿法 - C 语言
// 平方根运算 - 牛顿法
// a 为非负数
int SqrtNewton(int a) {
if (a == 0) return 0;
double x = a; // 初始值起为 a 本身
double d = 0.0;
do {
// delta 是 f(x) / f'(x) 即 (x^2 - a) / (2x)
// 防溢出,写作如下方式
d = x / 2 - a / x / 2.0;
if (d < 1e-6) break; // 假设误差是 1e-6
x -= d;
} while (x - a / x > 0);
return x;
}
相关阅读: 基本数论类算法 - 辗转相除和素数筛
(完)
本文原始链接地址: https://hit9.dev/post/algorithm-basic-math-computations
