This article records algorithms for some basic mathematical operations.
The content includes:
This article contains a lot of content, and requires the reader to read it calmly.
Integer Addition ¶
Without using the four arithmetic operators (addition, subtraction, multiplication, and division), how can addition be implemented programmatically?
LeetCode problem - Add Without Plus Sign
Review the familiar columnar calculation of decimal addition:
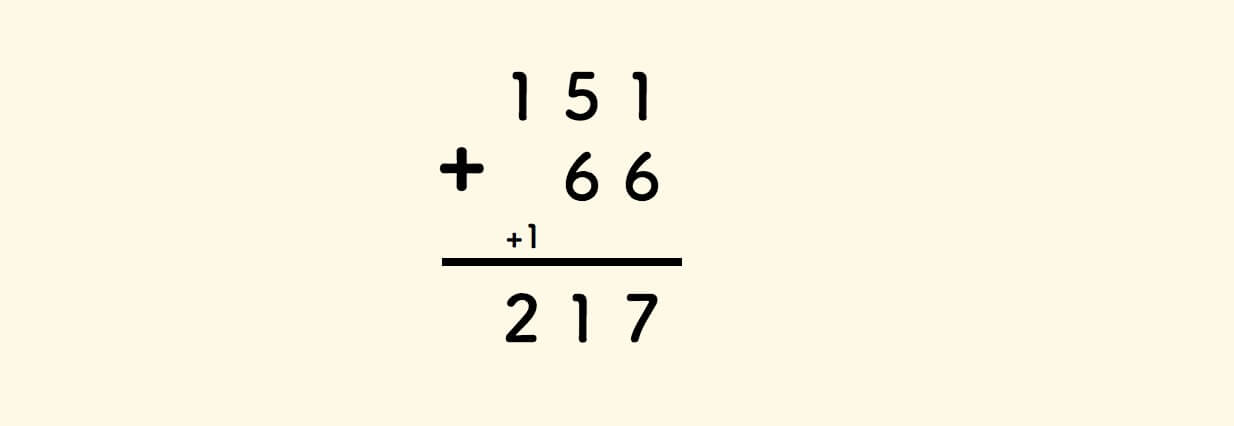
Binary addition is similar, carry over on reaching two:
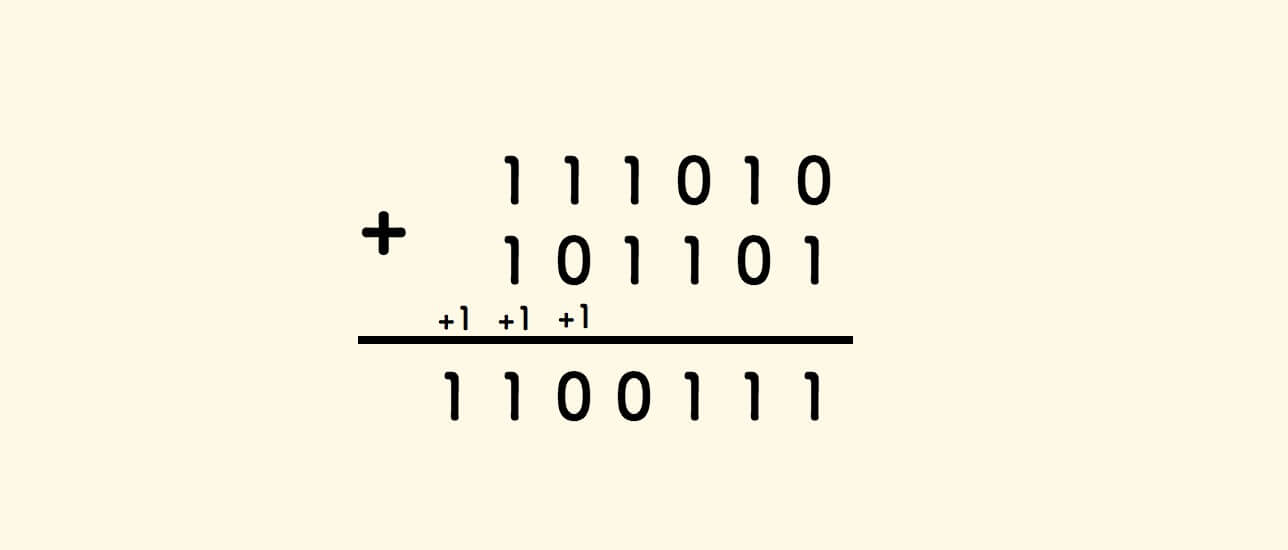
Denote the carry column as c, and the sum without considering carry as s.
If the sum of the bit values in the previous position reaches two, then the next position’s c is recorded as 1, and s only records the bit value of the sum of the current position.
In this way, the above binary columnar calculation can be broken down as follows:

It can be seen that the columnar calculation is iteratively performed until the carry c is 0. At that time, s is the final calculation result.
On each column, the calculation table for the next bit’s c and the current bit’s s is as follows:
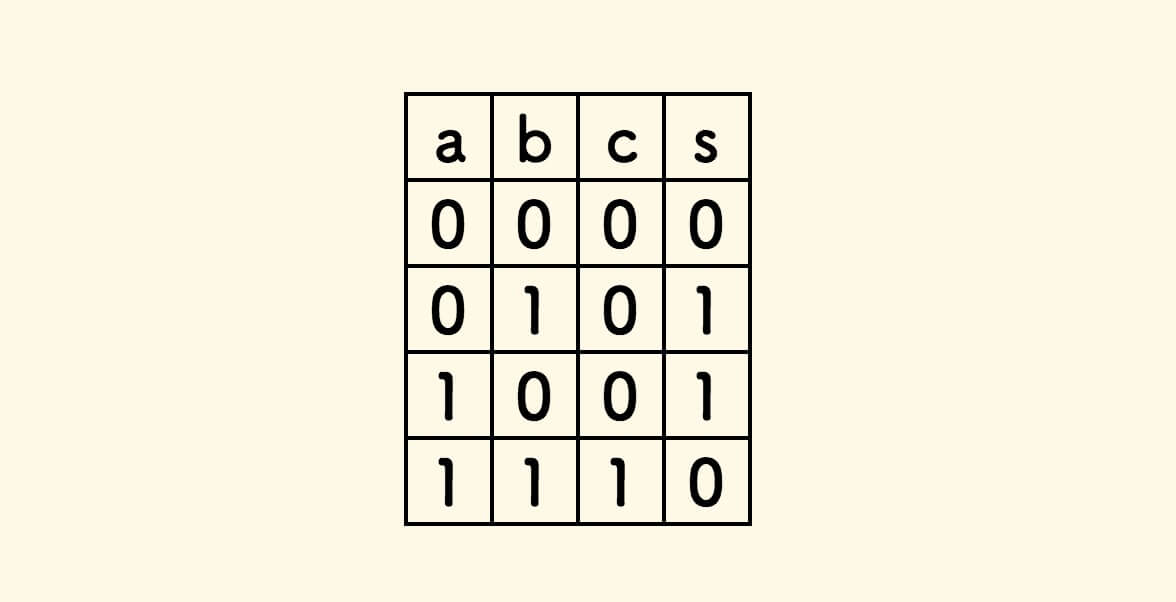
Careful observation reveals that the value of c is actually the result of a “logical AND”, and the value of s is actually the result of a “logical XOR”:
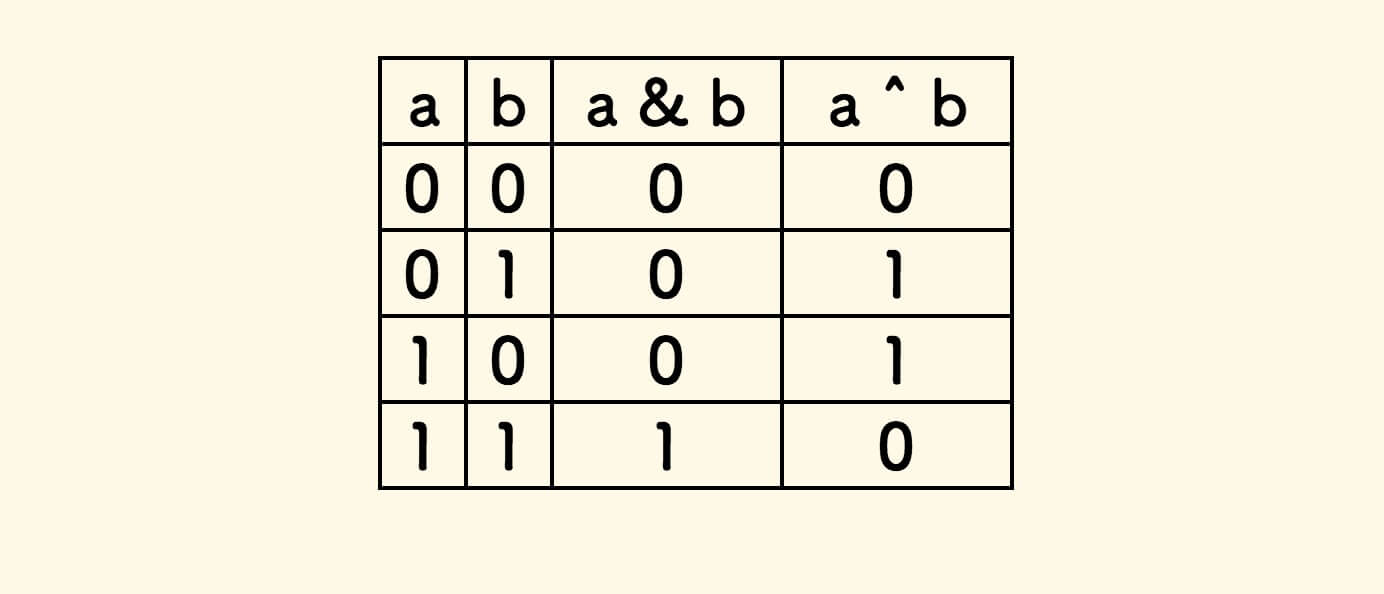
Therefore, the value of c can be expressed as (a & b) << 1, and the value of s can be expressed as a ^ b.
After calculating c and s each time, treat c as the new a, and s as the new b, and keep looping and iterating until a is 0, then the final calculation result b is obtained.
Does this method hold for negative integers? The highest bit of a negative number is the sign bit 1. Below is the result of the 8bit negative integer -1 and 23 = 10111:
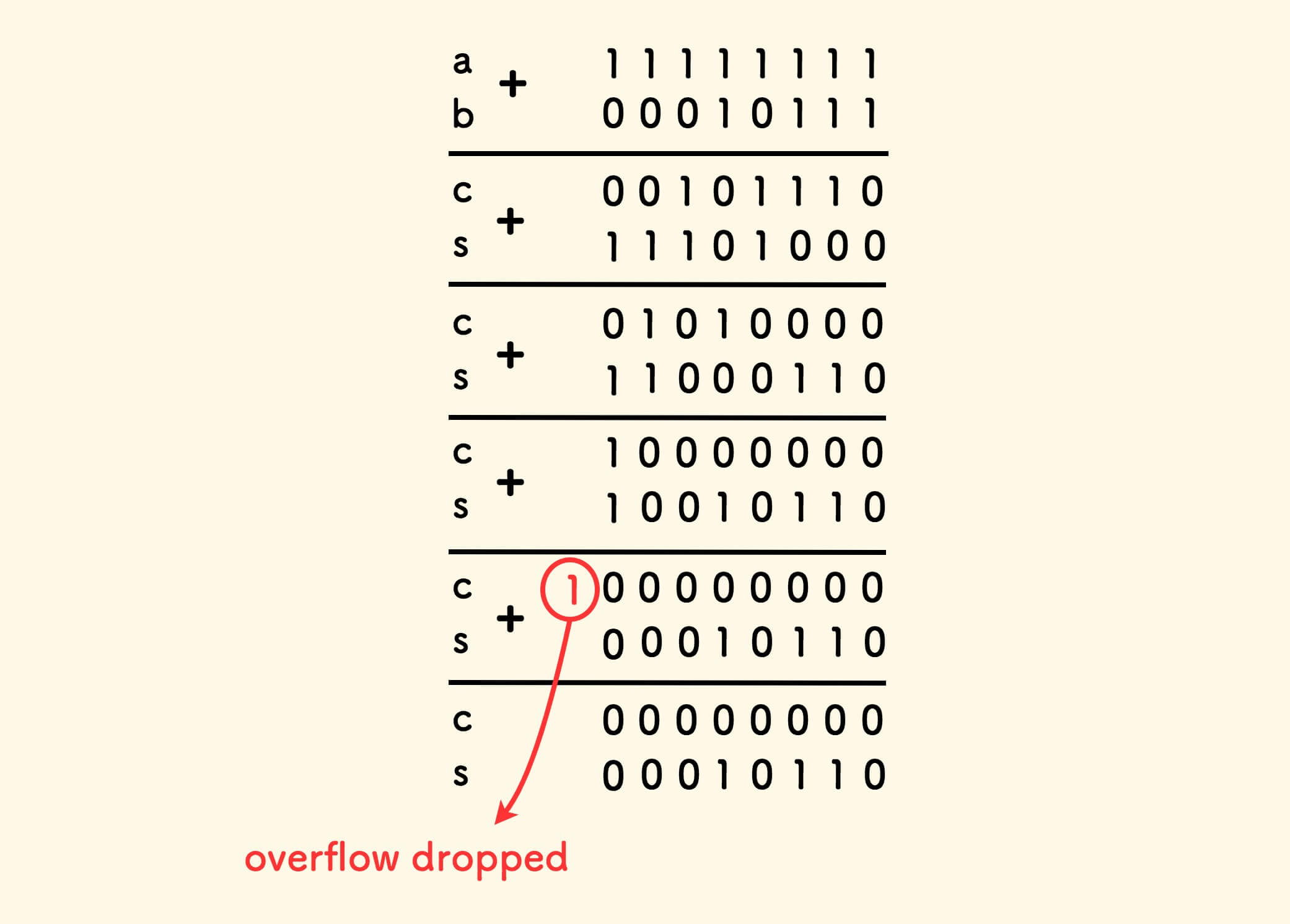
The algorithm still applies. In fact, in binary, a negative number is nothing more than a large positive number.
Bitwise Operation Implementation of Addition - C Language
// Addition
int Add(int a, int b) {
do {
int c = (unsigned int)(a & b) << 1;
int s = a ^ b;
a = c;
b = s;
} while (a != 0);
return b;
}
In the above algorithm, each left shift takes O(k) time, where k is the larger number of bits of the two integers.
In the worst case, when there are the most carry bits. The following is an example diagram of the worst-case scenario of the algorithm in the case of a 4bit integer. The process of calculating -1 plus 1 requires 4 steps to complete.

For a 32bit signed integer, the worst case requires 32 steps to complete.
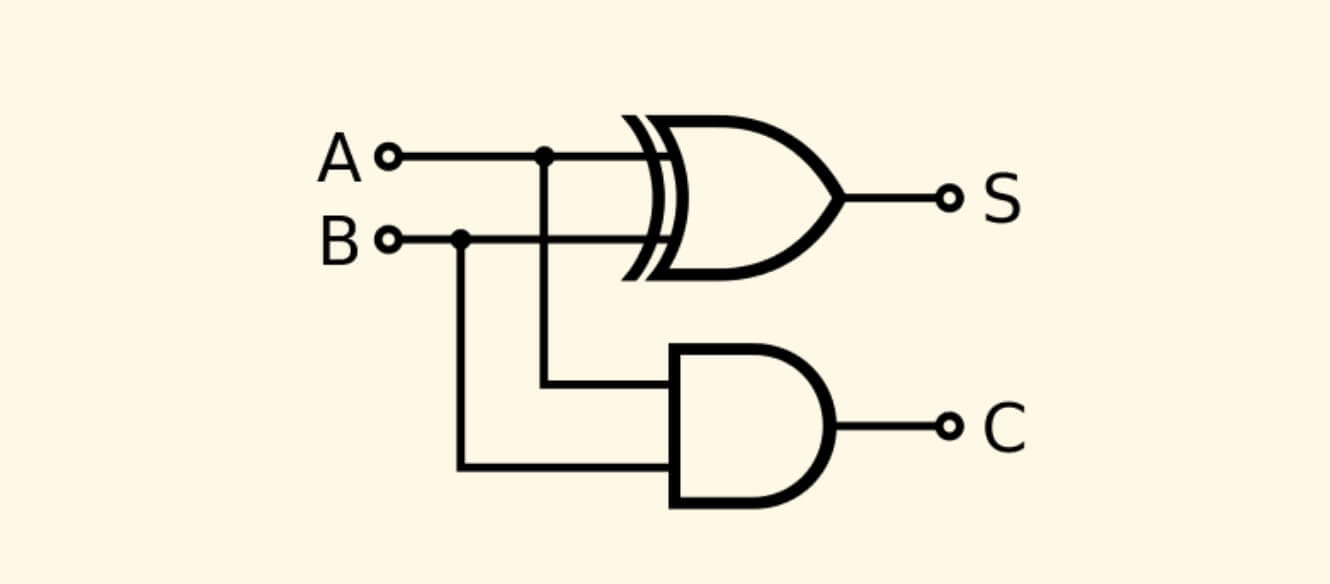
In fact, this method is very similar to the implementation of an adder in a computer.
A one-bit half adder receives two bits of input, outputs the sum S of the current bit through an XOR gate, and outputs the carry C through an AND gate.
Integer Subtraction ¶
Subtraction can be expressed using addition: a - b = a + (-b).
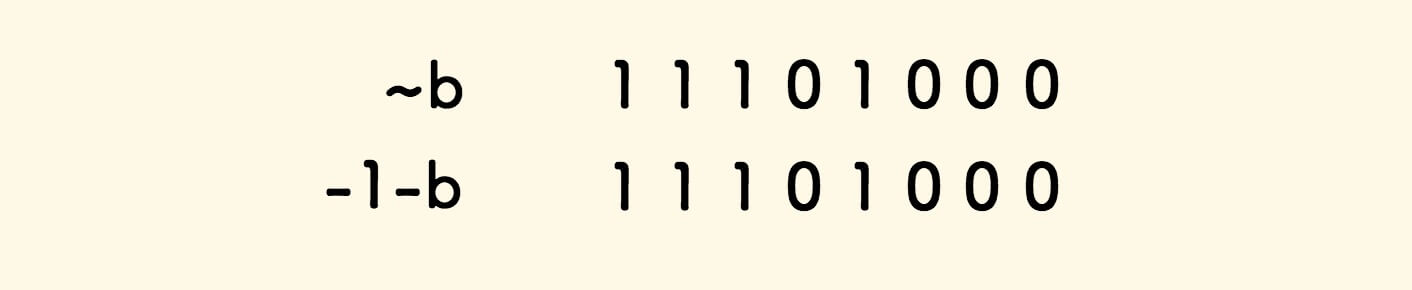
Taking an 8bit signed integer as an example, if b = 10111, then -b can be derived as follows:

Also, since -1-b is actually ~b, so -b = ~b+1.
Therefore a - b = a + (~b+1), that is, Minus(a, b) = Add(a, Add(~b, 1)).
Bitwise Operation Implementation of Subtraction - C Language
// Subtraction
int Minus(int a, int b) { return Add(a, Add(~b, 1)); }
Integer Multiplication ¶
Multiplication is iterative addition. However, if calculated in this way, the time complexity is O(min(a,b)).
Iterative Addition Implementation of Multiplication O(min(a,b)) - C Language
#define MIN(a, b) (a) > (b) ? (b) : (a)
#define MAX(a, b) (a) > (b) ? (a) : (b)
// Multiplication - Simple method O(min(a,b))
// Assume that addition has been implemented
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int MulNaive(int a, int b) {
int min = MIN(a, b);
int max = MAX(a, b);
int r = 0;
while (min-- != 0) r += max;
return r;
}
A faster way is the bisection method (binary splitting).
For example, the calculation process of 13x17 can be broken down as follows:
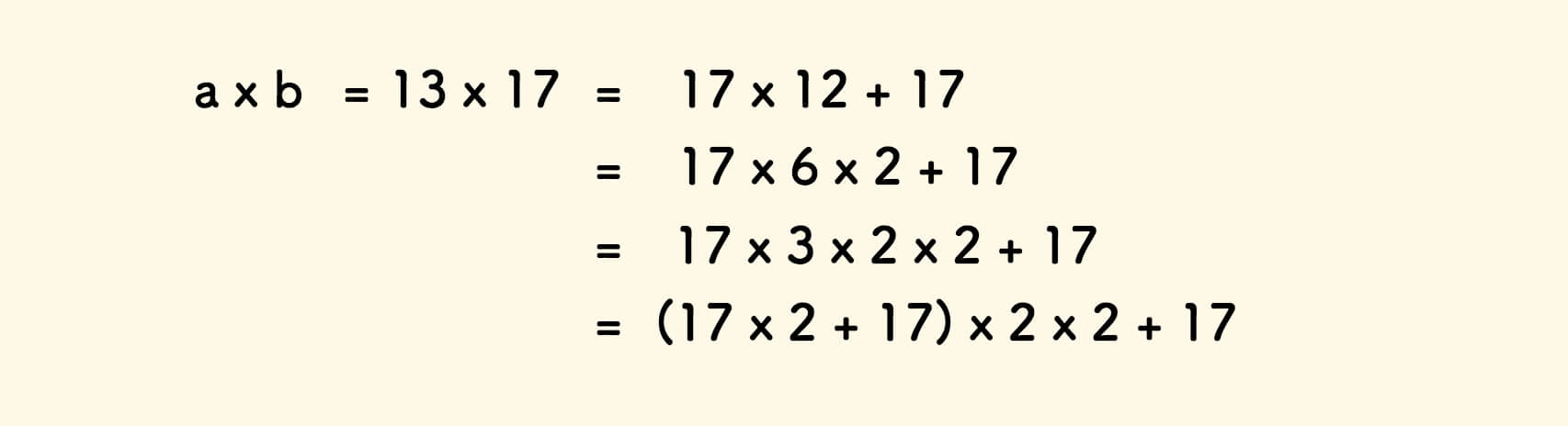
In the process of decomposition, a is treated as a multiple, and b is treated as a multiplicand.
If the multiple is an even number, bisect the multiple, otherwise turn the multiple into an even number.
It is easy to derive the recursive version of this method:
Bisection Implementation of Multiplication - Recursive Version - C Language
// Multiplication - Bisection method Recursive version
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int MulRecursive(int a, int b) {
int min = MIN(a, b);
int max = MAX(a, b);
if (min & 1) // Odd number
return MulRecursive(min - 1, max) + max;
else { // Even number, note min/2 is min >> 1
int half = MulRecursive(min >> 1, max);
return half << 1; // That is half x 2
}
}
Another perspective is to decompose a x b into three parts:
- Calculation result
result - Multiplication factor
factor - Remaining multiple
remain
The construction method is in the form of a x b = result + factor * remain.

Try to continuously reduce the remaining multiple:
- If it is an even number, decompose a
2into the multiplication factorfactoron the left, that is,factorincreases by a factor of two, and the remaining multiple is halved. - If it is an odd number, decompose a multiplicand
factorand add it to theresulton the left, and the remaining multiple is reduced by one.
When the remaining multiple is reduced to 0, result accumulates to the final result.
The following is the best case for this algorithm, where the remaining multiple is continuously halved:
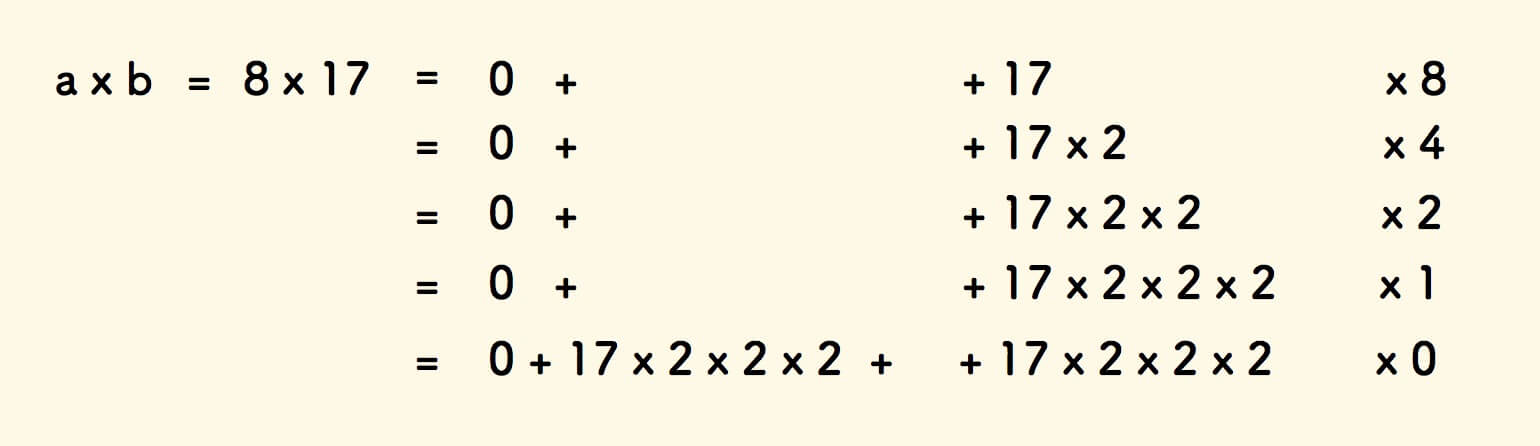
Bisection Implementation of Multiplication - Iterative Version - C Language
// Multiplication - Binary method iterative version
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int MulBinary(int a, int b) {
int min = MIN(a, b); // The smaller one is used as a multiple
int max = MAX(a, b); // The larger one is used as a multiplicand
int r = 0; // Calculation result
int factor = max; // Multiplication factor
int remain = min; // Remaining multiple
while (remain != 0) {
if (remain & 1) {
// The remaining multiple is odd
r += factor;
remain--;
} else {
remain >>= 1; // The remaining multiple is halved
factor <<= 1; // The multiplicand is doubled
}
}
return r;
}
Obviously, the time complexity is O(logn), where n is the smaller of a and b.
The last idea is to recall the columnar multiplication of decimal numbers:
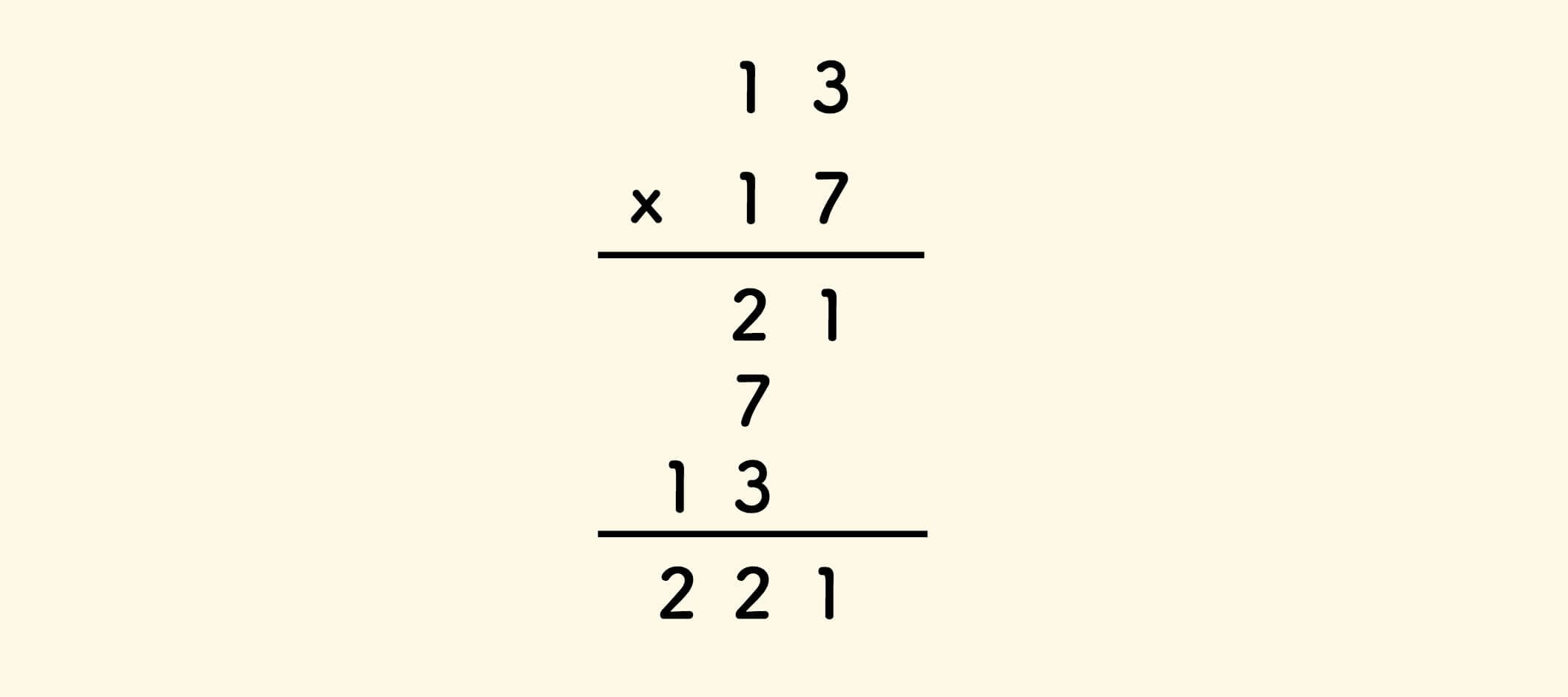
The columnar multiplication of binary numbers is like this:
Compared with decimal multiplication, it is simpler. 0 multiplied by any number is 0, and 1 multiplied by any number is itself. There is no need for the multiplication table:
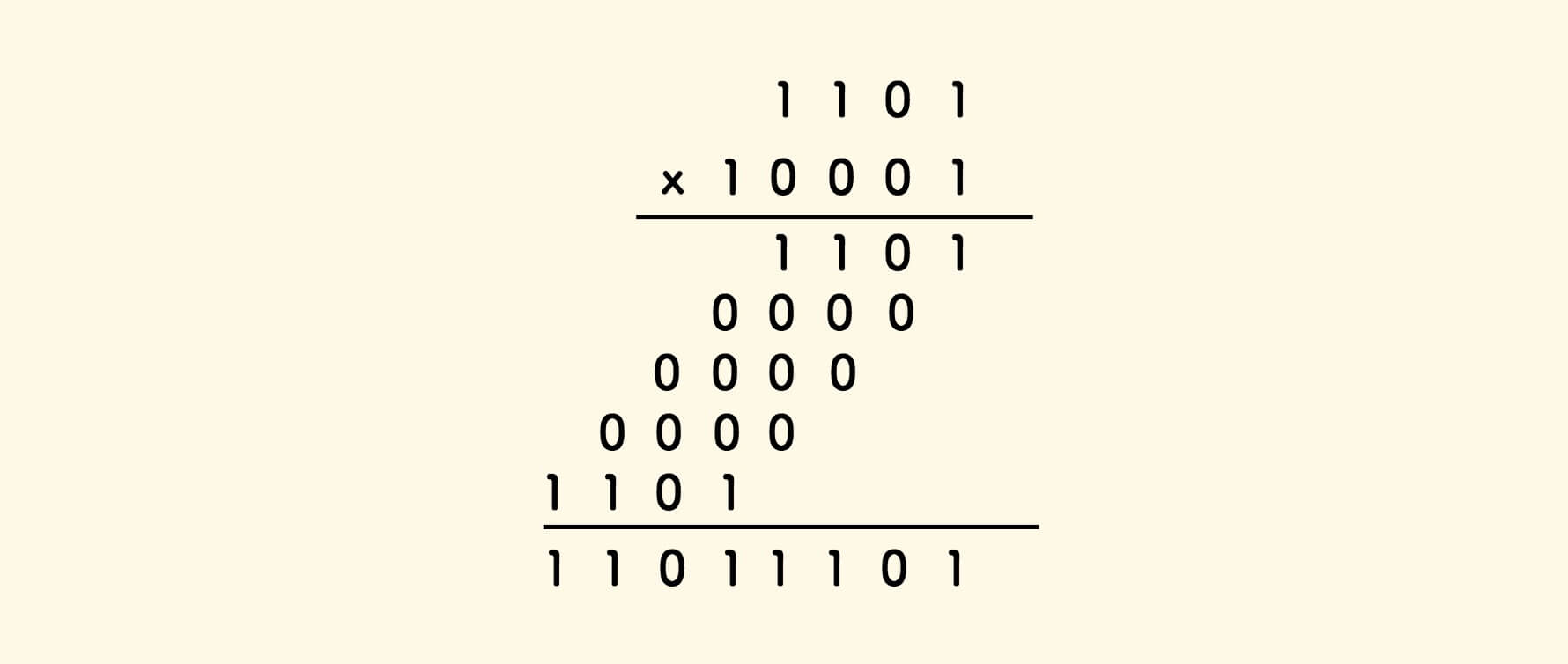
Assume that the number of bits of a and b are k and m. The sum of the numbers obtained by continuously shifting a number b to the left k times is the multiplication result.
Specifically:
- Continuously shift the number
ato the right until it is0. That is, it has movedktimes. - After each right shift of the number
a, its current last digit isa & 1, multiply it by the numberb:0multiplied by any number is0, so there is no need to deal with this situation.1multiplied by any number is itself, only this situation needs to be handled.- Shift the product to the left by one bit and add it to the calculated result for summation.
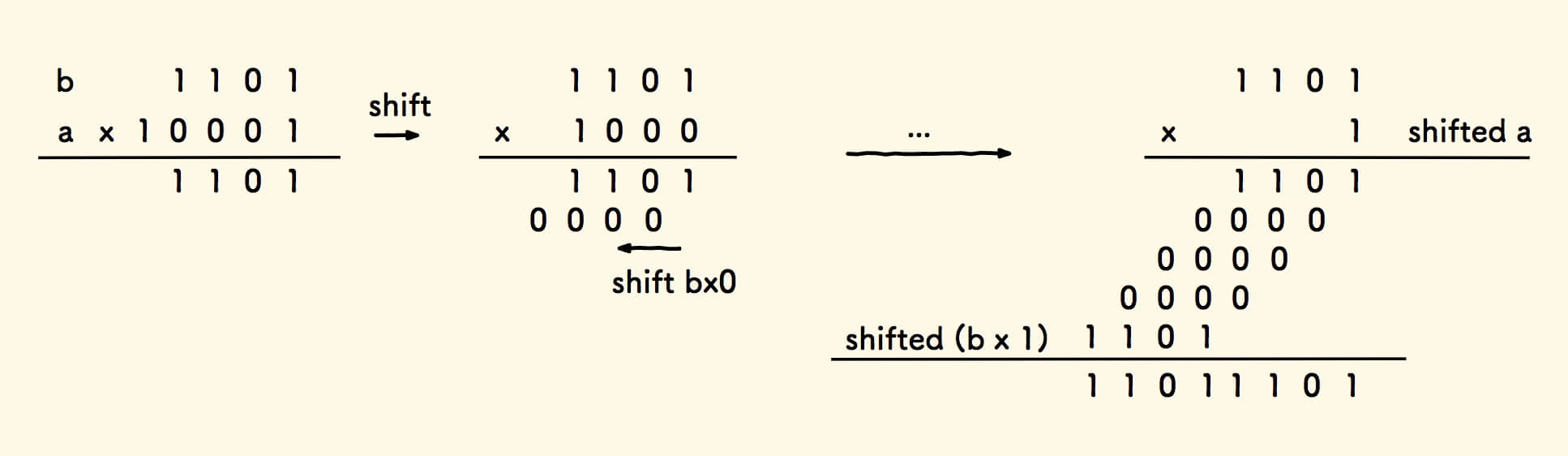
This yields the so-called fast multiplication algorithm.
Implementation of the Binary Columnar Idea for Multiplication - C Language
// Multiplication - Columnar calculation method
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int MulFast(int a, int b) {
int r = 0; // Multiplication result
while (a != 0) {
if (a & 1) {
// The current bit is 1, 1 multiplied by any number is itself
// Add b at this time
r += b;
}
// Otherwise, the current bit is 0, 0 multiplied by any number is 0, no need to add
a >>= 1; // Moving k times to 0 means that a has k bits
b <<= 1; // Shift b to the left synchronously
}
return r;
}
It is easy to know that the time complexity of this algorithm is O(k), where k is the number of bits of the integer a.
Note that all multiplication time complexities mentioned here are in terms of ignoring the overhead of addition time.
Integer Division ¶
LeetCode problem - Divide Two Integers
Similar to the analysis idea of multiplication, the easiest way is to transform division into a cyclic subtraction.
The O(n) time complexity algorithm is omitted here.
Considering the result of 255 / 17, similar to multiplication, decompose the calculation formula into the following form:
Where:
- The coefficient of the factor to be subtracted
factor: increase by a factor of two each time. Ifremainis insufficient,factorresets to1. - The remaining dividend
remain: the remaining part after the dividend is continuously subtracted. - The calculation result
result: increases by the size offactoreach time.

Terminate the algorithm process when the remaining part of the dividend remain is less than the size of b.
Bisection Implementation of Division - C Language
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int Div(int a, int b) {
int remain = a;
int factor = 1;
int bfactor = b; // b x factor.
int result = 0;
while (remain >= b) {
if (remain < bfactor) {
// The dividend is not enough to subtract, reset factor
factor = 1;
bfactor = b;
}
remain -= bfactor;
result += factor;
// factor x2
factor = factor << 1;
// bfactor x2
bfactor = bfactor << 1;
}
return result;
}
The time complexity is O(logn).
Another idea comes from the columnar division formula.
Review the columnar division calculation method of decimal numbers:
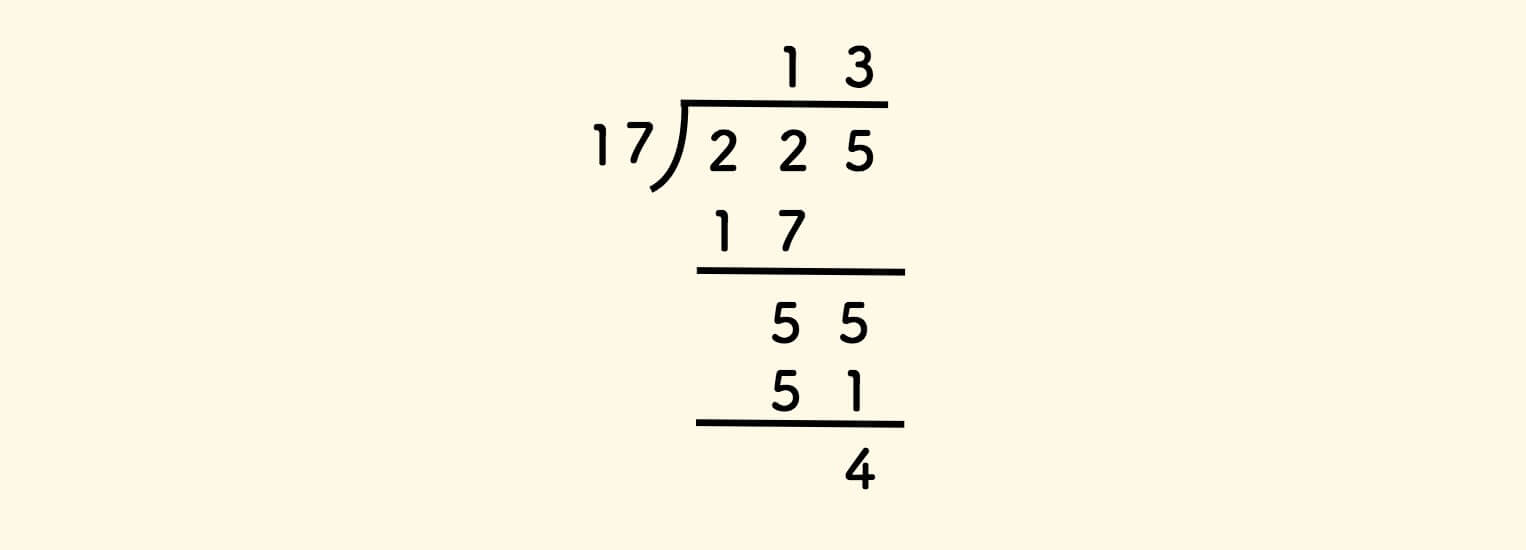
Binary columnar division is also the same:
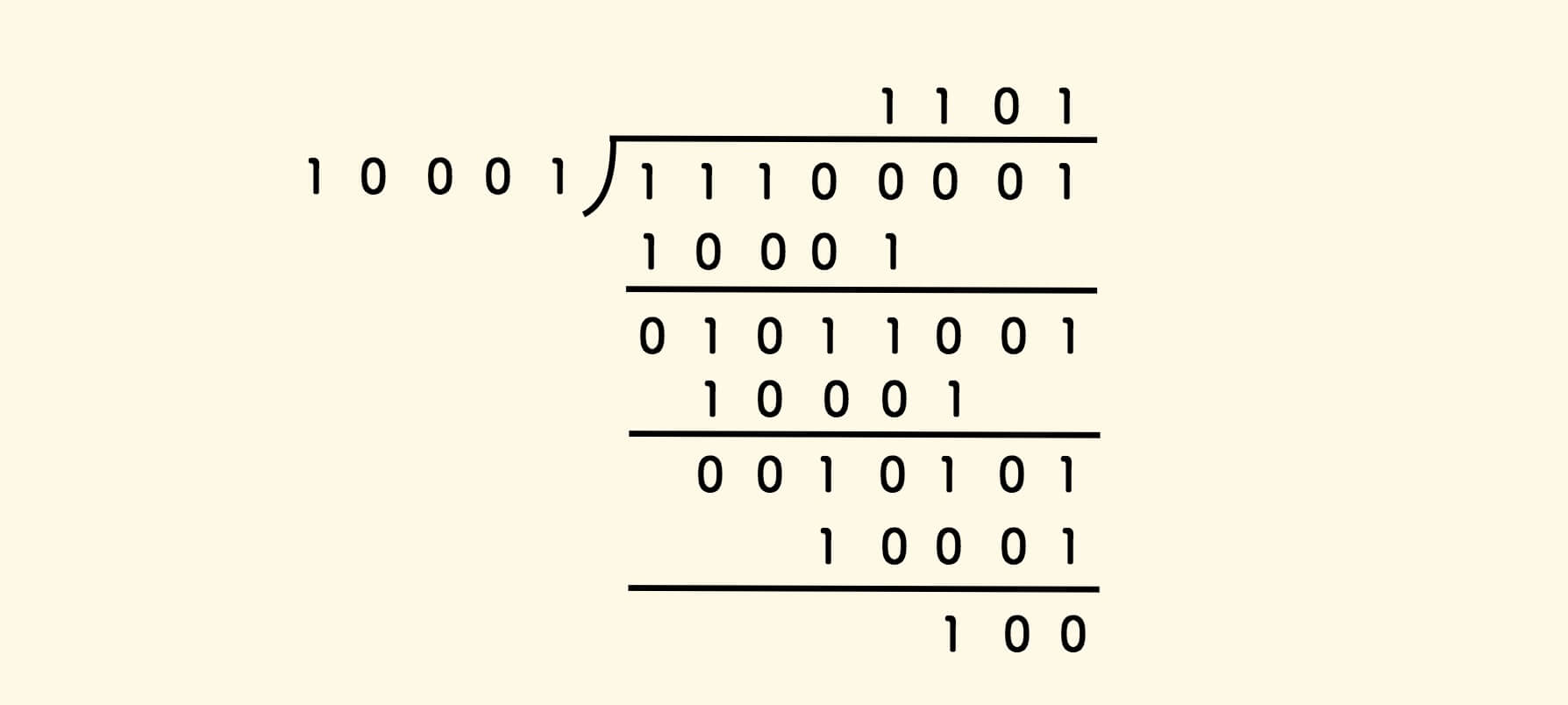
The idea of the algorithm is:
- Initialization,
ris the division result. - Left-align the effective bit starting bits of
aandb. - If, after alignment,
bis not greater thana, then update the dividenda = a-b, and mark the current bit ofras1. - Otherwise, mark the current bit of
ras0. - End the calculation until the two numbers are right-aligned.
The time complexity of this algorithm is O(k), where k is the number of bits of the two integers.
Implementation of the Columnar Idea for Division - C Language
// Get the number of bits of a given integer
int GetNBits(int a) {
int n = 0;
while (a) {
a >>= 1;
n++;
}
return n;
}
// Division Columnar Calculation
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int DivFast(int a, int b) {
int n = GetNBits(a);
int m = GetNBits(b);
int r = 0; // Calculation result
for (int i = n - m; i >= 0; i--) {
// Shift b to the left to align the current a
int b1 = b << i;
if (b1 <= a) {
// Mark the i-th bit of the result as 1
r |= (1 << i);
a -= b1;
}
// Otherwise, mark the current bit of r as 0, that is, no need to set
}
return r;
}
Note that all division time complexities mentioned here are in terms of ignoring the time overhead of addition and subtraction.
Fast Power (Exponentiation) ¶
The fast power algorithm is similar to the analysis idea of multiplication mentioned earlier.
Taking 3^13 as an example, expand as follows:
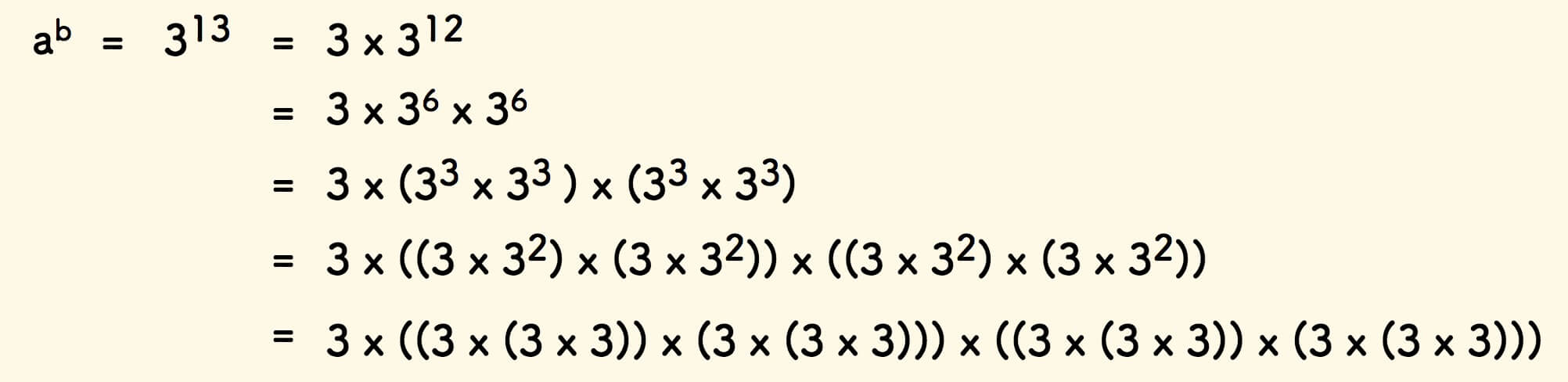
It is easy to derive the recursive version of the bisection method:
Recursive Version of the Bisection Method for Power Operations - C Language
// Power Operation - Binary Recursive Version
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int PowRecursive(int a, int b) {
if (b == 0) return 1;
// Odd number
if (b & 1) return PowRecursive(a, b - 1) * a;
// Even number
else {
int half = PowRecursive(a, b / 2);
return half * half;
}
}
The time complexity is O(logb), where b is the power.
However, the following method with an iterative approach is more wonderful.
Consistent with the decomposition idea of multiplication, write a^b in the form of result * (factor) ^ remain:

- If the remaining exponent
remainis odd, then decompose a factorfactorand give it to theresulton the left. - Otherwise, split
remainin half, andfactordoubles by self-multiplication.
When the remaining exponent remain reaches 0, result gets the result.
Iterative Version of the Bisection Method for Power Operations - C Language
// Power Operation - Binary Iterative Version
// The following only considers the implementation of positive numbers, and negative numbers can be converted to positive numbers for processing
int PowFast(int a, int b) {
int factor = a;
int result = 1;
int remain = b;
while (remain > 0) {
if (remain & 1) {
// Odd number
result = result * factor;
remain--;
} else {
// Even number
remain = remain / 2; // The remaining exponent is split in half
factor = factor * factor; // The factor doubles by self-multiplication
}
}
return result;
}
The time complexity is still O(logb), where b is the power.
Note that the time complexity of all power operations mentioned here is in terms of ignoring the time overhead of multiplication and division.
Fast power often comes with a modulo operation. Below is the implementation of PowFastMod:
Binary Iterative Version of Power Operations - C Language
// Fast power with modulo operation
// Note that the modulo operation satisfies the distributive law for multiplication (x*y)%m=(x%m * y%m)%m
int PowFastMod(int a, int b, int mod) {
int factor = a % mod;
int result = 1;
int remain = b;
while (remain > 0) {
if (remain & 1) {
// Odd number
result = result * factor % mod;
remain--;
} else {
// Even number
remain = remain / 2; // The remaining exponent is split in half
factor = factor * factor % mod;
; // The factor doubles by self-multiplication
}
}
return result % mod;
}
Square Root ¶
How to solve for the value of $\sqrt a$? Given $a >= 0$.
Since the function $x^2$ is monotonically increasing in the interval $x >= 0$, the bisection method can be used. It is not much different from standard binary search, so the introduction is omitted.
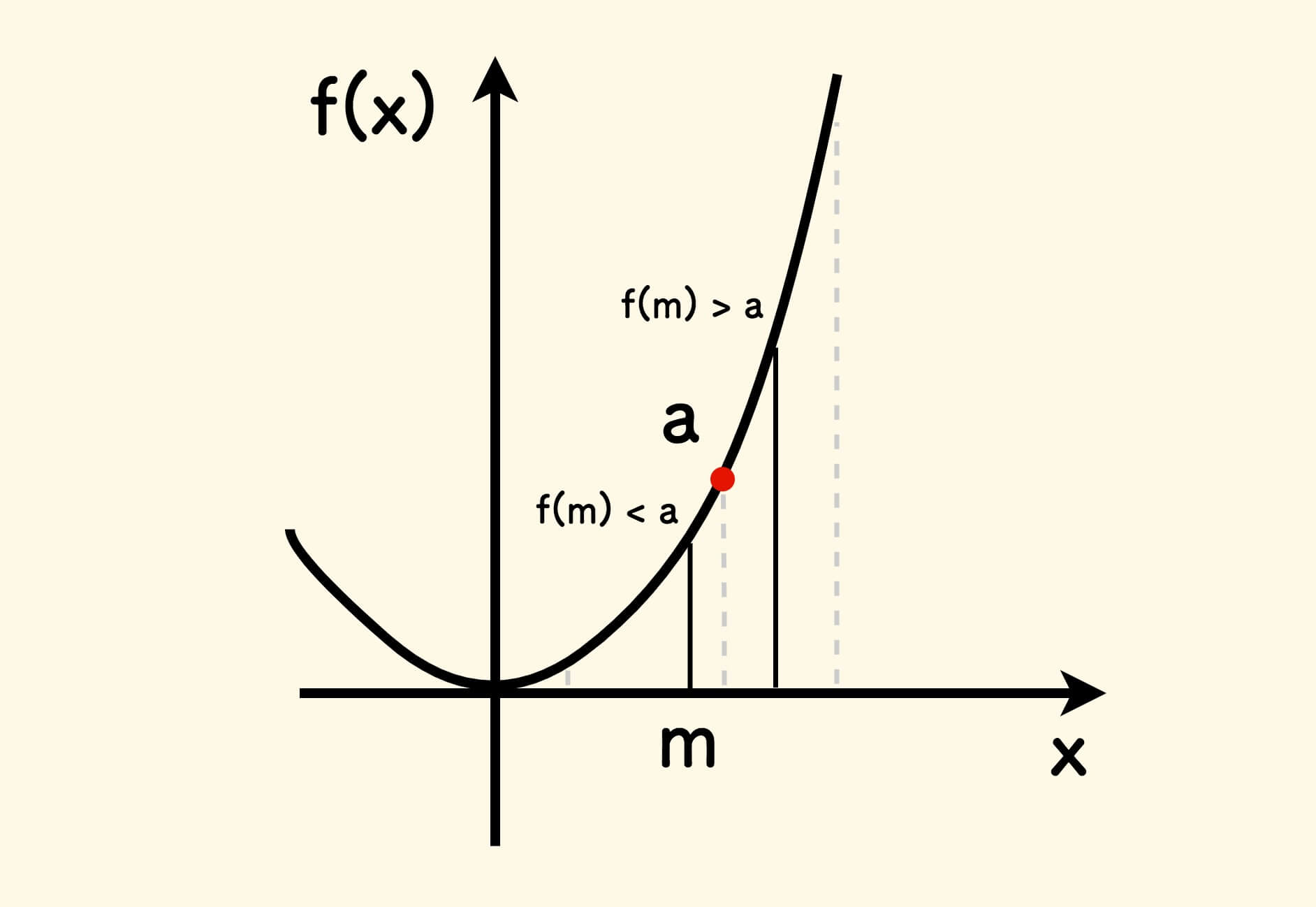
Square Root Operation - Bisection Method - C Language
// Square root operation - Bisection
// a is a non-negative number
int Sqrt(int a) {
if (a == 0) return 0;
if (a == 1) return 1;
int l = 0;
int r = a;
while (l < r) {
int m = (l + r) / 2;
if (m < a / m) { // Do not use m * m < a to prevent overflow
l = m + 1;
} else if (m > a / m) {
r = m - 1;
} else {
return m;
}
}
// The found l may be slightly larger than the actual value
if (l > a / l) return l - 1;
return l;
}
In numerical analysis, there is a common method for finding the approximate zero value of a function: Newton’s method.
Solving for the value of $\sqrt a$ is actually solving for the zero value of the function $f(x) = x^2 - a$.
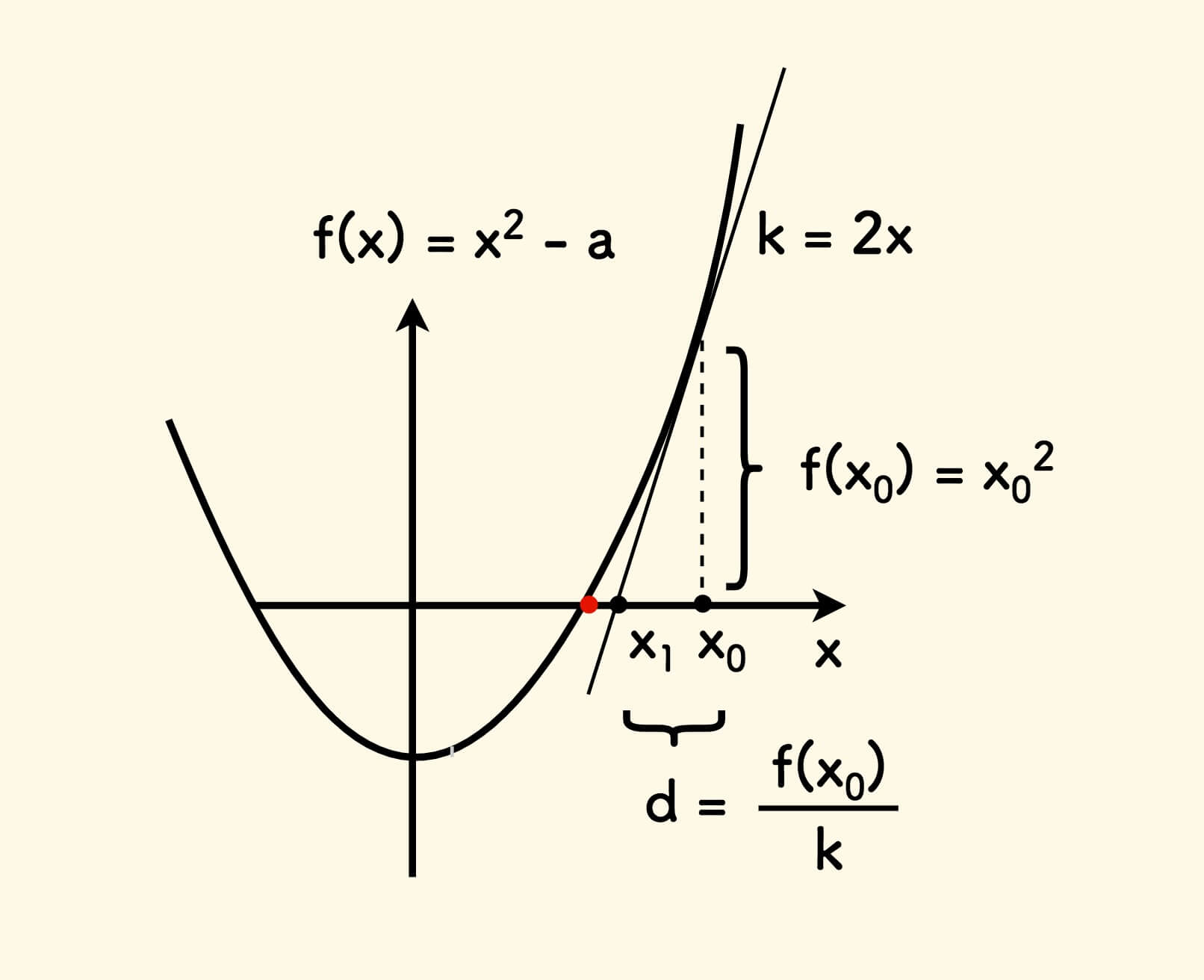
The idea of Newton’s method is to first take a value $x = x_0$, then draw the tangent of the function at this point, and use the intersection point $x_1$ of the tangent and the horizontal axis as The new value of $x$ is continuously iterated until the error between $f(x)$ and zero meets the accuracy requirements.
The slope $k$ of the tangent can be calculated from the derivative of the function $f’(x) = 2x$, that is, $k = 2x_0$. Therefore:
\[x_1 = x_0 - \frac {f(x_0)} {f'(x_0)}\]Iterate in this way.
Square Root Operation - Newton's Method - C Language
// Square root operation - Newton's method
// a is a non-negative number
int SqrtNewton(int a) {
if (a == 0) return 0;
double x = a; // The initial value starts at a itself
double d = 0.0;
do {
// delta is f(x) / f'(x) that is (x^2 - a) / (2x)
// In order to prevent overflow, write as follows
d = x / 2 - a / x / 2.0;
if (d < 1e-6) break; // Assume the error is 1e-6
x -= d;
} while (x - a / x > 0);
return x;
}
Complete code in this article on Github
Related reading: Basic Number Theory Algorithms - Greatest Common Divisor and Prime Number Sieves
(End)
Please note that this post is an AI-automatically chinese-to-english translated version of my original blog post: http://hit9.dev/post/algorithm-basic-math-computations.
Original Link: https://hit9.dev/post/en/algorithm-basic-math-computations